面向农业温室环境的ICDO-RBFNN多传感器数据融合算法

罗焕芝; 王骥

doi:10.11975/j.issn.1002-6819.202402013

面向农业温室环境的ICDO-RBFNN多传感器数据融合算法

罗焕芝,
王骥^,

1.
广东海洋大学电子与信息工程学院，湛江 524088
2.
广东省智慧海洋传感网及其装备工程技术研究中心，湛江 524088

基金项目: 广东省普通高校重点领域新一代信息技术专项（2020ZDZX3008）

详细信息

作者简介:
罗焕芝，研究方向为智能检测与传感技术。Email：987299174@qq.com

通讯作者:
王骥，教授，硕士生导师，研究方向为无线传感器网络、海洋物联网与人工智能。Email：13902576499@163.com

中图分类号: S625.5+1；TP183
计量
- 文章访问数: 137
- HTML全文浏览量: 12
- PDF下载量: 74
出版历程
- 收稿日期: 2024-02-02
- 修回日期: 2024-08-18
- 网络出版日期: 2024-09-29
- 刊出日期: 2024-11-14

ICDO-RBFNN multi-sensor data fusion for agricultural greenhouse environment

LUO Huanzhi,
WANG Ji^,

1.
School of Electronics and Information Engineering, Guangdong Ocean University, Zhanjiang 524088, China
2.
Guangdong Engineering Technology Research Center of Intelligent Ocean Sensor Network and Equipment, Zhanjiang 524088, China

摘要

摘要:
为改善农业环境传感器测量数据精度低、可靠性差的问题，该研究提出一种改进的切诺贝利灾难优化器（improved Chernobyl disaster optimizer，ICDO）优化径向基函数神经网络（radial basis function neural network，RBFNN）多传感器数据融合算法。首先引入佳点集、拉普拉斯交叉算子和修改位置更新方程改进切诺贝利灾难优化器（Chernobyl disaster optimizer，CDO），增强算法的寻优能力；再利用ICDO优化RBFNN模型，提升模型的稳定性；最后通过RBFNN模型的非线性映射能力实现多传感器数据融合方法，提高数据融合精度。仿真试验结果表明，大气环境质量预测的拟合优度达到0.999，均方误差低至0.348，平均绝对百分比误差降到0.729%；现场试验结果表明，温室环境等级划分的准确率高达99.21%，精准率为99.91%。研究提出的多传感器数据融合算法精度高，相对误差低，稳健性好。
- 温室 /
- 多传感器 /
- 数据融合 /
- ICDO /
- RBF神经网络
Abstract:
Agricultural sensors can greatly contribute to future technologies and systemic innovation in smart agriculture. However, the types and precision of sensors are limited to monitoring the agricultural environment with complex and diverse objects. The large and redundant monitoring data has also resulted in the low reliability of information perception. In this study, an improved radial basis function neural network (RBFNN) and Chernobyl disaster optimizer (ICDO) multi-sensor data fusion was proposed to improve the accuracy and reliability of single-sensor measurement. Firstly, an improved Chernobyl catastrophe optimization was performed on the neural network model. The good-point set theory was introduced to improve the initial population quality of the CDO, particularly for accuracy and speed. The adaptive Laplacian crossover operator was added to enhance the search performance. The better adaptive behavior was achieved in the high convergence speed. And then, the individual learning and differential evolution strategy were used to redefine the location update equation, in order to balance the local and global exploration. Secondly, the RBF neural network model was optimized by ICDO, in order to improve the stability of the model. Finally, the nonlinear mapping of the RBF neural network model was used to realize the multi-sensor data fusion with high accuracy. Three experiments were conducted to verify the improved model. The first one was to verify the ICDO. A large improvement was obtained in the solution accuracy and optimization stability, compared with particle swarm optimization (PSO), gray wolf optimization (GWO), firefly algorithm (FA), dung beetle optimizer (DBO), and subtraction average-based optimizer (SABO). The second one was to evaluate the quality of the atmospheric environment. Specifically, the atmospheric data was collected outside the South Subtropical Botanical Garden in Mazhang District, Zhanjiang City, Guangdong Province, China, from September 1, 2022, to September 30, 2023. The goodness of fit reached 0.999 for the prediction of atmospheric environmental quality, the mean square error was as low as 0.348, and the mean absolute percentage error was reduced to 0.729%. The third one was to classify the greenhouse environment. The data was collected in the greenhouses of the South Asian Tropical Botanical Garden. The accuracy rate of greenhouse environment classification was 99.21% with a precision rate of 99.91%. The data fusion was suitable for both indoor and outdoor environments, indicating better adaptability and high accuracy. This finding can also provide solid technical support to agricultural sensor data fusion in the field of precision agriculture.
- greenhouse /
- multi-sensor /
- data fusion /
- improved Chernobyl disaster optimizer /
- RBF neural network

HTML全文

0. 引　言

中国作为传统农业大国，温室大棚的出现有效解决了作物生长受外部条件限制的难题。为提升设施农业生产的效率，温室内通常种植密集，作业空间狭小，且耕、种、管、收全周期的工作任务繁重。此外，温室中的高温、潮湿和密闭环境对人体健康产生不利影响，不适宜人工长时间作业^[1-4]。温室机器人的应用为解决这些问题提供了一种有效途径，然而温室内复杂且有限的空间要求机器人具备高效的路径规划能力，并能够在避免与障碍物碰撞的前提下完成任务。由于地面粗糙度变化，温室机器人的底盘（以下简称“机器人底盘”）可能会受到不同程度的垂直脉冲应力，这些应力会损坏电池的内部结构，如隔膜撕裂、电极结构受损等，进而缩短电池寿命。如果路径规划仅考虑避免大面积粗糙地面，可能会导致行驶路径过长，从而降低工作效率和能源利用率。因此，寻找兼顾能源高效利用与路径优化的规划方法，对于减少温室气体排放^[5-6]和实现能源政策目标至关重要。

路径规划的研究通常分为3种主要方法：传统方法、深度学习方法和强化学习方法，其中传统全局路径规划算法在实际应用中非常广泛^[7-11]。沈跃等^[12]提出了一种基于相邻争夺（adjacent competition，AC）算法的植保无人机作业路径规划算法，该算法首先对粒子设置作业距离范围，其次在范围内对粒子作业距离初始值进行随机分配，最后通过相邻粒子争夺作业距离来搜索最优路径，此算法不仅解决了传统粒子群（particle swarm optimization，PSO）算法在规划植保作业路径时易陷入局部最优、搜索能耗最优方案能力低等问题，同时也保证了作业总距离一定、对搜索方向进行先验且不遗漏特殊点，提高了植保无人机作业效率、减少了无人机损耗。孙月平等^[13]提出了一种基于改进A*算法与人工势场法相融合的蟹塘投饵船动态路径规划算法（fusion of improved A* and artificial potential field，FIA*-APF），通过引入动态加权因子优化A*算法评价函数、加入转折惩罚函数等方法，在静态和动态仿真环境及蟹塘试验中，FIA-APF算法在规划时间、指令节点数量、路径长度及转角等方面表现出色；然而，该算法的缺点在于计算量大、灵活性不足、难以适应复杂动态环境变化，并且对先验知识依赖程度高，这使得在复杂温室环境中构建先验知识模型变得困难，导致无法实现最优的路径规划。

深度学习可以用来对路径规划所涉及的环境进行建模和理解，通过对大量数据进行特征提取和数据分析，从而提高路径规划的效率和结果。DANG等^[14-15]提出了一种基于单目摄像机的移动机器人实时避障策略，该方法使用二值语义分割单目摄像机捕获的图像来提取特征，并估计机器人环境中障碍物的位置和距离。然后，基于增强A*算法的优化路径规划，结合碰撞、路径、平滑代价等加权因子，来提高移动机器人的路径规划性能。孙国祥等^[16]为解决传统温室导航方案的路径规划问题，提出了基于即时定位与地图构建技术的激光视觉融合式自主导航算法，利用多种设备和算法实现局部与全局定位及自主导航，满足了温室高精度建图、定位和导航需求。但是深度学习在规划效果上仍存在一些不足，其根本原因是路径规划方面存在计算量大、硬件需求高、模型设计复杂、可解释性差、对数据依赖强且易受数据质量影响等缺点，并且在温室环境中还可能面临实时性不足、难以适应动态变化环境以及训练和调试难度大等问题。

强化学习是一种通过与环境交互进行自我更新的方法^[17-19]，能适应复杂动态环境，注重长期回报，并具有良好的可扩展性和通用性。LAZZARONI等^[20]探讨了一种基于深度强化学习的智能体，能够同时执行路径规划和轨迹执行，处理传感器感知信息，并像普通驾驶员一样直接控制方向盘和加速器。他们将研究对象限制在低速运动和狭窄的可行驶区域内，该智能体完全依赖传感器所捕获的实时信息作为输入参数来取消对地图的依赖。结果显示智能体在目标到达率和换挡次数方面均优于传统的混合A*路径规划算法。但该研究仅对规划效果进行了优化，未充分考虑到地面粗糙度变化对机器人电池寿命的影响以及能源效率的需求，同时，DRL是基于传统QL的贪心算法进行单步长梯度优化，易产生局部最优、收敛效率低以及训练慢等问题。

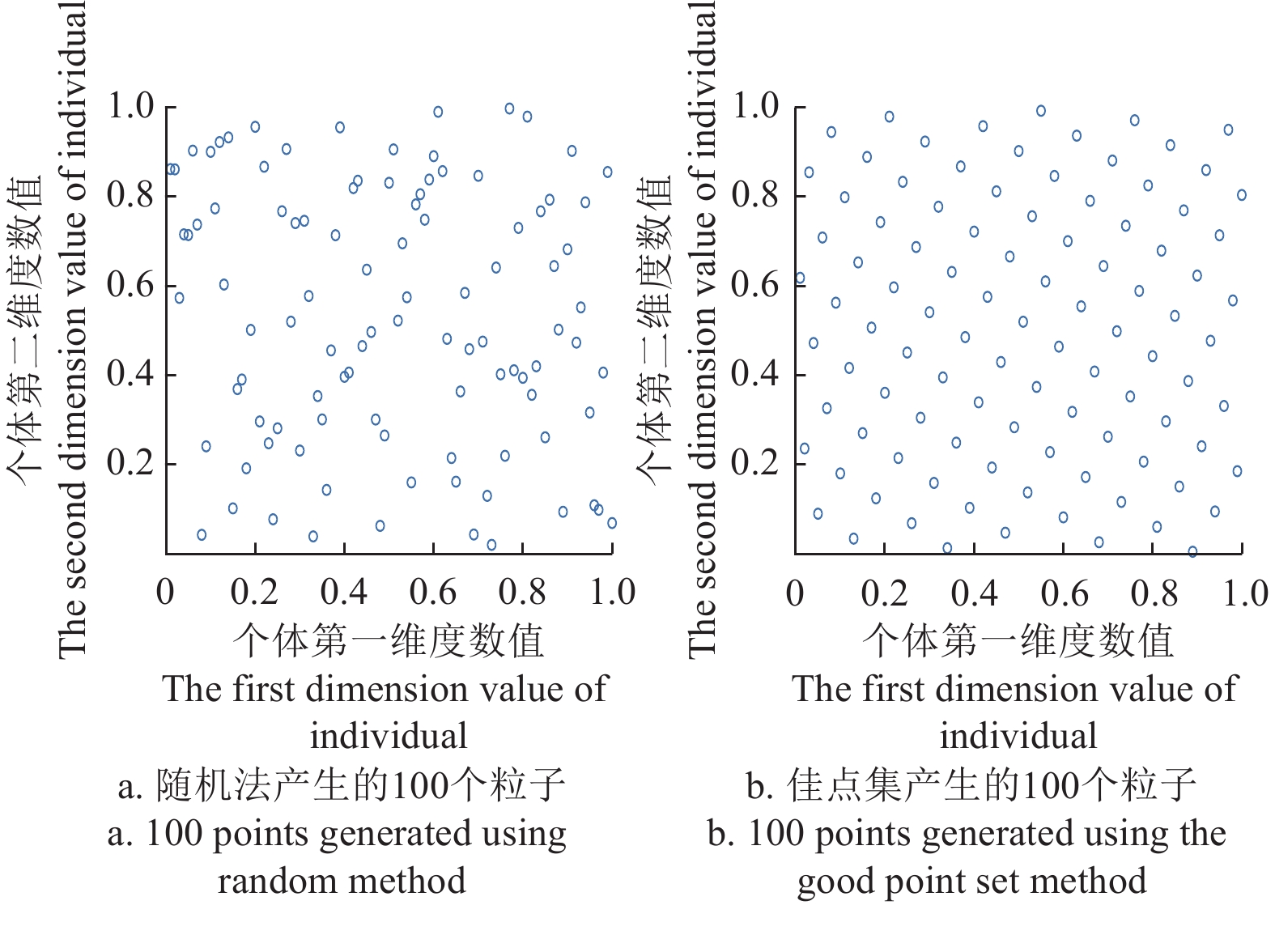
针对以上问题，本文基于强化学习对温室机器人底盘的路径规划算法进行研究。一方面，温室环境复杂且空间有限，强化学习能够让温室机器人底盘通过与环境不断交互自主完成路径规划的工作，并在避免与障碍物碰撞的同时提高路径规划的效率。另一方面，考虑到地面粗糙度变化对机器人底盘电池寿命以及电池利用效率的影响，强化学习可以通过定义合适的奖励函数，确保温室机器人底盘在规划路径时会权衡因行驶路线过长导致工作效率、能源利用率的降低和因在大粗糙地面行驶导致电池寿命缩短之间的关系，并确定出最优路线。同时，针对传统Q-Learning(QL)的单步长梯度优化导致易陷入局部最优、收敛效率低以及训练慢等问题，本文提出并探讨了AMQL、AEQL、AMEQL算法的优点和适用性，以期为温室机器人底盘自主路径规划提供理论参考。

1. 传统QL算法

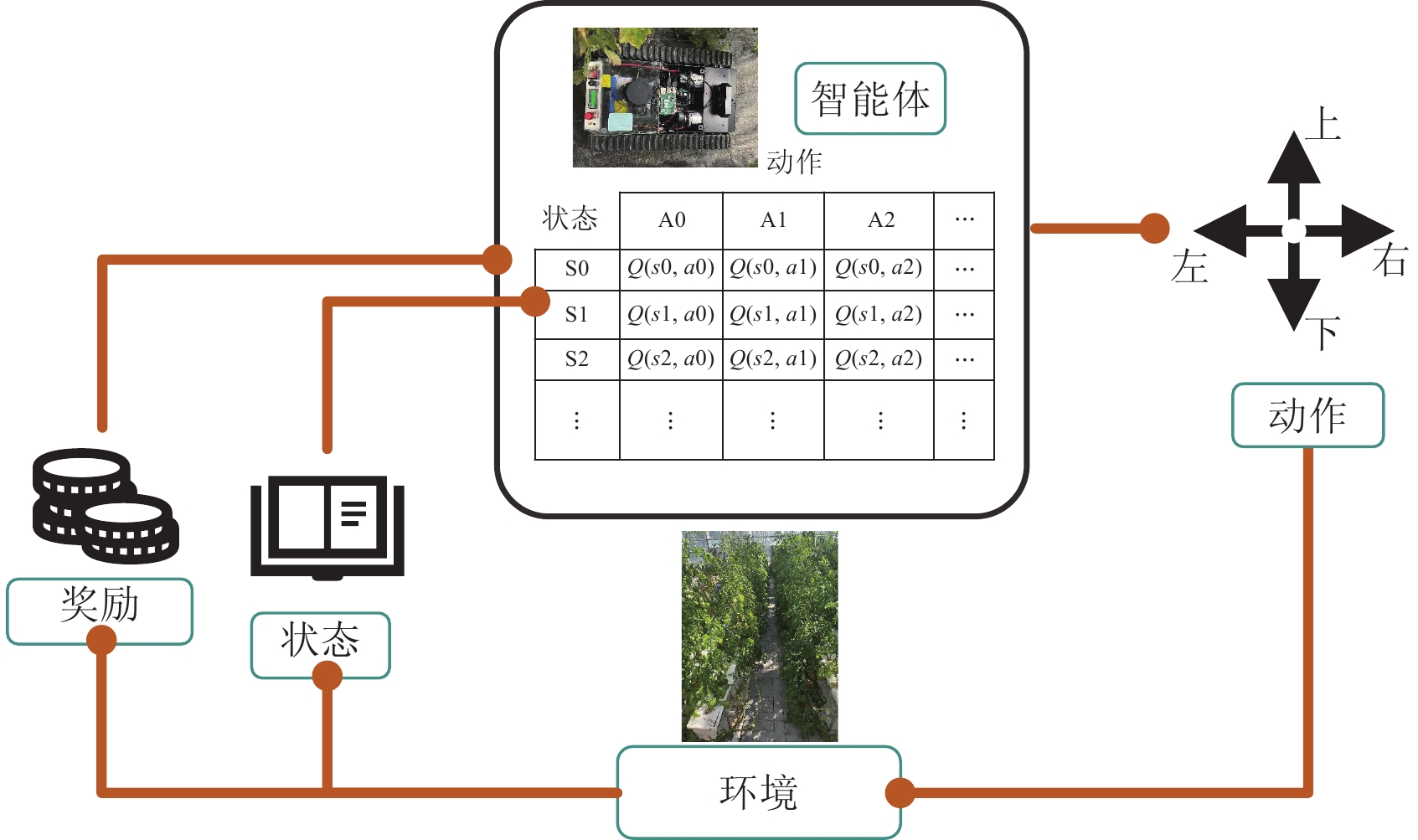
传统QL是一种基于价值迭代的强化学习算法，用于解决马尔可夫决策过程（markov decision process，MDP）中的最优控制问题^[21-22]。与基于模型的强化学习方法不同，Q-Learning不需要事先了解环境的完整动态模型，就能通过与环境交互的方式进行学习。同时，Q-Learning具有一定的鲁棒性，即使目标位置存在偏差，所学习的策略仍能在一定程度上保证任务的顺利完成。该算法通过训练智能体在特定环境中选择最优行动，从而最大化累积预期奖励。作为强化学习中的一种基于价值的算法（value-based），Q-Learning通过计算Q值，即在状态s（s∈S）下采取动作a（a∈A）时的预期收益，来指导智能体的决策。该算法的核心思想是通过计算Q值来构建Q表存储各状态-动作（S-A）对Q的值，并依据Q值选择最优动作，如表1所示。

表 1 部分存储Q值的Q表

Table 1. Partial Q-table for storing Q-values

状态Status	A1	A2
S1	Q（s1,a1）	Q（s1,a2）
S2	Q（s2,a1）	Q（s2,a2）
S3	Q（s3,a1）	Q（s3,a2）
注: Q（s1,a1）表示在状态S1下做动作A1的Q值，余同。
Note: Q(s1, a1) represents the Q value of taking action A1 in state S1， the following as the same.

下载: 导出CSV

| 显示表格

算法的核心计算式-贝尔曼方程如式（1）所示：

$Q(s,a) \leftarrow Q(s,a) + \alpha [\gamma \cdot {\max _{a{'}}}Q({s^{{'}}},{a^{{'}}}) - Q(s,a)]$

(1)

式中 $s$ 是当前状态， $a$ 是当前动作， ${s^{{'}}}$ 是转移到的下一个状态， ${a^{{'}}}$ 是转移状态之后执行的动作， $\gamma$ 是学习率（控制Q值更新的步长）， $\alpha$ 是折扣因子（用于平衡当前奖励和未来奖励的重要性）。该算法利用时间差分方法，将蒙特卡罗采样与动态规划中的自举技术相结合，使其成为一种无需环境模型的算法。通过自举机制，算法利用后继状态的值函数来估计当前状态的值函数，实现单步更新。这种方法不仅避免了对完整环境模型的依赖，还显著加快了学习速度。通过更新Q值来优化策略，使得机器人在不断探索环境的同时最大化累积奖励，图1为算法流程图。

图 1 传统QL算法流程图

Figure 1. Flow chart of the traditional QL algorithm

下载: 全尺寸图片幻灯片

2. 强化学习能量管理策略

通过对实际场景的考察发现，不同垄道中泥土和沙砾导致地面粗糙度存在明显差异，如表2所示，不同的地面粗糙度对电池的工作效率和寿命产生了显著影响^[25-28]。鉴于温室地面的复杂性，本文基于强化学习的能量管理进行路径规划。在此过程中，首先需要学习先验的专家知识，作为强化学习奖励设置的基础。该先验知识主要包括两部分：电池在不同地面粗糙度下的寿命以及利用效率的使用情况。机器人底盘实车坐标系如图2所示。

表 2 地面粗糙度

Table 2. Ground roughness

地面覆盖物 Ground cover	粗糙度 Roughness （Z₀）/m	预打分奖励 Pre-scoring reward		颜色表示 Color indication
地面覆盖物 Ground cover	粗糙度 Roughness （Z₀）/m	电池寿命 Battery life	电池利用率 Battery utilization efficiency	颜色表示 Color indication
城郊房舍区（Level 1）	0.60	0.167	1.67	绿色
牧场（Level 2）	0.20	0.5	5	黄色
谷草地（Level 3）	0.10	1	10	紫色
长草地、石头摊（Level 4）	0.050	2	20	蓝色
注：通过对参考文献[23-24]提取level1～level4四个不同粗糙度地面以实现分级预打分。
Note: Four different roughness levels of ground, namely level1 to level4, were extracted from references [23-24] to achieve graded pre-scoring.

下载: 导出CSV

| 显示表格

图 2 车辆坐标系

Figure 2. Vehicle coordinate system

下载: 全尺寸图片幻灯片

2.1 电池寿命与电池利用效率先验知识

1）电池寿命

SOMERVILLE等^[29]采用在振动测试期间对电池进行X射线光电子能谱分析的方法，研究了锂离子电池因振动引起性能退化的机电机制。结果表明，振动导致电池表面选择性形成的膜被去除，并由电解质分解产生的新表面膜所取代。这种由振动引发的膜层变化是电池性能退化的主要原因。

2）电池利用效率

ZHANG等^[30]研究了振动对锂离子电池的直流电阻、1C容量以及一致性的影响。用统计学方法研究了锂离子电池试验数据，通过对32个18650电池单轴振动获取数据，借由大样本量剖析了测试前后电池直流电阻和容量的方法变化。结果表明，在95%的置信水平下，振动致使直流电阻显著上升，同时也能观察到1C容量有所降低。

振动导致电池内阻增加和容量减小，会对电池利用效率产生多方面的明显影响。首先，内阻增加会导致电池在放电过程中更多的电能被转化为热能而散失掉，即能够实际用于驱动设备或完成其他工作的电能减少，电池利用效率降低。其次，电池可提供的总电荷量减少，原本能够支持机器人底盘运行较长时间的电池，由于容量降低，其使用时间会大幅缩短。最后，内阻增加和容量减小还可能导致电池的输出功率不稳定。在温室环境中，这可能会引起机器人底盘性能的下降，甚至出现故障。

2.2 先验知识分级预打分机制

通过电池寿命与电池利用效率先验知识可知，地面粗糙度越大，对电池寿命以及电池利用效率的影响越明显。因此，本文通过学习相关先验知识，为不同粗糙度地面进行分级预打分，其打分机制如式（2）~（3）所示。由于车载惯性测量单元（inertial measurement unit，IMU）可以实时获取地面粗糙度数据，分级预打分可以为不同地面粗糙度数据提供相应的先验奖励，因此机器人底盘可借助IMU实时获取这些奖励数据，在后续的强化学习中，这些奖励将有助于寻找最优路径。

${e_{(i)}} = 1/{Z_o}$

(2)

${l_{(i)}} = 1/{Z_o} \cdot H$

(3)

式中 ${e_{(i)}}$ 与 ${l_{(i)}}$ 为不同粗糙度地面分级预打分奖励，即粗糙度越大奖励值越低。l₍_i₎为电池寿命在不同地面粗糙度下的分级预打分， ${e_{(i)}}$ 为电池利用效率在不同地面的分级预打分， ${Z_o}$ 为粗糙度， $H$ 为权重因子，由于粗糙度对电池寿命的影响更加明显^[31]，本文设置 $H$ 为0.1以减少对奖励的影响。

2.3 外部环境及底盘奖励函数模型

为了实现机器人底盘在作业时的能量管理控制，需要根据不同地面粗糙度和底盘状态进行合理的路径规划，进而使机器人底盘能够在避开高粗糙度地面的同时，提高电池的有效利用率。由于强化学习在训练的初始阶段无法直接做出正确的决策，而是通过不断试错来获取奖励值并进行优化，最终形成有效的训练模型，以确保机器人底盘的行为符合多系统动态协调控制的要求。然而，逐一将不同动作作用于车辆动力学模型并计算对应的奖励值，该过程过于繁琐，且车辆动力学模型中许多部分与奖励值计算并无直接关联。因此，需建立一个能够准确模拟机器人底盘在接收到上层控制指令后不同动作表现的环境模型，作为强化学习算法的训练环境。在实际验证中，将整车的状态作为输入，动作作为输出，具体步骤如下：

首先，设计奖励函数：1）根据机器人底盘在不同地面粗糙度环境下的电池利用效率和寿命表现，设置对应奖励数值，鼓励机器人底盘选择更加高效的电池使用方式；2）根据机器人底盘的路径规划表现，设置对应距离的奖励函数，鼓励其选择更加高效的路径。

其次，基于以上两种补充情况，在底盘执行动作后评估其行为并进行反馈，将相应的奖励分配给机器人底盘。对于正向行为，通过给予正向奖励的方式增加这些行为的发生频率；对于负向的行为，通过给予负向奖励的方式减少这些行为的发生频率。

最后，通过机器人底盘与环境的持续交互、学习和调整，使其能够根据奖励反馈逐步优化行为策略，从而实现更高效的能量管理控制，并提升电池的使用效率和寿命。

本文将奖励函数 ${R_{(i)}}$ 设计为基于不同地面粗糙度下的电池使用效率、电池寿命以及运行路径长度这3个因素有关的函数，具体如式（4）所示。

${R_{(i)}} = \omega \cdot {e_{(i)}} + \beta \cdot {l_{(i)}} + \mu \cdot d$

(4)

其中d为运行路径（用曼哈顿距离表示）， $\omega$ 、 $\beta$ 、 $\mu$ 为权重因子，通过设置权重来优化温室机器人底盘在规划路径时避免大粗糙度地面以提高电池寿命、增加电池利用效率，同时缩短行驶路程以减少工作时间等多个目标。

3. Q-Learning算法优化

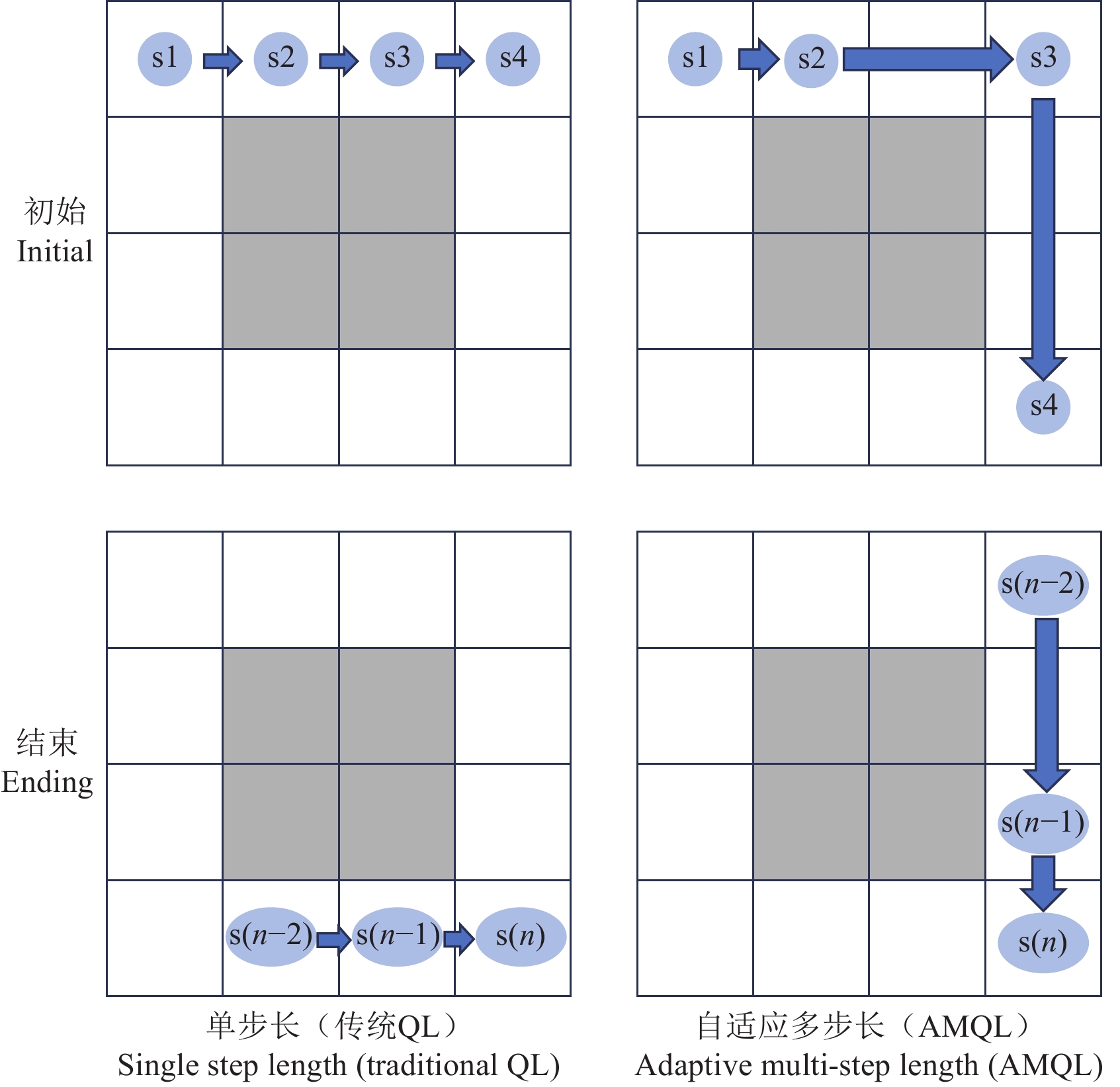
3.1 改进的自适应多步长QL算法（AMQL）

传统QL算法在大型状态空间中的收敛速度通常较慢，尤其当状态空间包含大量随机性因素或者存在长期延迟现象时。为解决这一问题，本文构建了AMQL的优化方法。AMQL是指在QL算法中采用自适应的步长，以提高算法的效率和收敛性，并且大幅减少拐点数量。传统的QL算法使用固定单步长向周围探索，但在实际应用中，步长的选择可能会对算法的性能产生重要影响。自适应多步长的QL算法可以根据学习过程中的反馈动态地调整步长，以更好地适应环境的变化和学习的进展，如图3所示。

图 3 AMQL算法流程图

Figure 3. Flow chart of the AMQL algorithm

下载: 全尺寸图片幻灯片

AMQL算法流程：

1）初始化动作a与状态s。

2）判断是否到达最大迭代次数。

3）若达到最大迭代次数，则输出训练完的最优路径；若未到达最大迭代次数的同时，未达到终止条件（最大步数），则继续根据当前的策略选择动作a。

4）执行上一步选择的动作a，观察环境反馈（奖励r和转移到的下一个状态s'）。

5）使用式（1）更新Q值。

6）判断环境所给予的奖励是否为正，如果在连续两个步长中都获得正向奖励，则认为当前搜索为正确路径，并且计算当前位置与目标点的曼哈顿距离。如果满足连续正向奖励且曼哈顿距离大于10（避免在探索终点时欠拟合），在下次探索时将步长增加为2。若持续获得正向奖励，则步长增加，最大可至5；如果满足连续正向奖励且曼哈顿距离小于10，则步长会根据距离的缩小自适应减少；若不满足上述条件，重置步长为1，如图4所示。

图 4 传统QL单步长与AMQL对比

注：图中n为时间步数。

Figure 4. Comparison of traditional QL single step length and AMQL

Note: In the figure, n is the number of time steps .

下载: 全尺寸图片幻灯片

7）循环执行步骤2）至步骤5），直到达到指定的停止条件。

3.2 改进的自适应ε -greedy的QL算法（AEQL）

ε -greedy是强化学习中常用的一种策略，用于在探索与利用之间进行权衡，特别是在Q-learning等基于值的方法中常被使用。

传统ε -greedy策略是在每次选择动作时，以 $\varepsilon$ 的概率随机选择一个动作（探索），以 $1 - \varepsilon$ 的概率选择当前估计最优的动作（利用）， $\varepsilon$ 在每一轮迭代完之后会将以线性化的方式进行递减。这种贪心策略的缺点为：虽然每个动作都有被选择的概率，但选择过程过于随机，某些状态-动作对本应达到全局最优，但由于初始化的影响，其被访问的概率较低，容易陷入局部最优。此外，迭代过程中，若 $\varepsilon$ 过大会导致过度探索；若 $\varepsilon$ 过小则会导致难收敛。

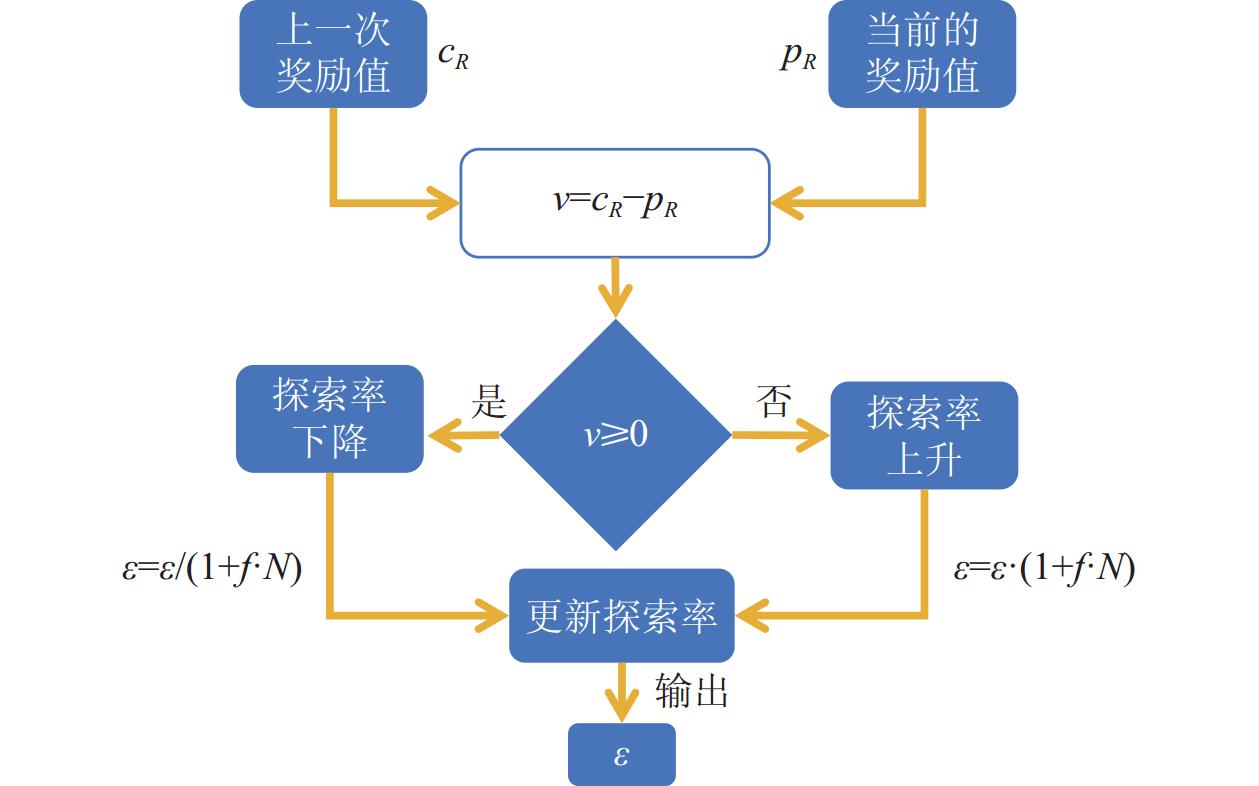
为解决上面问题，本文提出一种自适应 $\varepsilon$ 策略。通过式（5）~（8）来实现对 $\varepsilon$ 的动态调整。

$v = {c_R} - {p_R}$

(5)

$N = \frac{{{v_i} - {v_{\min }}}}{{{v_{\max }} - {v_{\min }}}}$

(6)

$\varepsilon \leftarrow \varepsilon /(1 + f \cdot N)$

(7)

$\varepsilon \leftarrow \varepsilon \cdot (1 + f \cdot N)$

(8)

式中 $v$ 表示奖励值变化率， ${c_R}$ 表示当前的奖励值， ${p_R}$ 表示上一次奖励值， $N$ 为归一化结果， ${v_i}$ 为当前的奖励值变化率， ${v_{\min }}$ 为最小奖励值变化率， ${v_{\max }}$ 为最大奖励值变化率， $\varepsilon$ 为探索度， $f$ 为权重。式（5）表示当前状态所获得的奖励值与上一个状态获得的奖励值之间的变化率。式（6）表示对当前获取的奖励值变化率进行归一化处理。式（7）表示当 $v$ 为非负值时 $\varepsilon$ 的迭代公式， $v$ 越大 $\varepsilon$ 减少的幅度越大， $v$ 越小 $\varepsilon$ 减少的幅度越小。式（8）表示当 $v$ 为负值时 $\varepsilon$ 的迭代公式， $v$ 越大 $\varepsilon$ 增大的幅度越大， $v$ 越小 $\varepsilon$ 增大的幅度越小。通过将 $\varepsilon$ 线性化递减的方式改变为依据奖励值的变化率来自适应实现对 $\varepsilon$ 的调整，更符合 $\varepsilon - greedy$ 算法的策略初衷，如图5所示。

图 5 自适应ε-greedy的Q-Learning优化流程图

Figure 5. Flow chart of Q-Learning optimization with adaptive ε-greedy

下载: 全尺寸图片幻灯片

3.3 算法融合（AMEQL）

AMQL算法与AEQL算法各有其优点，但也都存在明显的缺陷：虽然AMQL提高了收敛效率和迭代速度，但由于步长变化较大，导致奖励波动幅度很高，算法稳定性较低；同时，多步长的引入对收敛效率和迭代速度的提升效果并不十分明显；另一方面，AEQL通过动态调整 $\varepsilon$ 可以提高探索效率，增强算法稳定性，但由于 $\varepsilon$ 的在训练初期波动较大，增加了训练时间。为了解决这些问题，本文将AMQL与AEQL进行融合，提出融合算法AMEQL，此算法不仅解决了上述问题，而且结合了各自的优点，能够在全局路径规划中快速选择出更优的路径。其融合算法如图6所示。

图 6 融合算法流程图

Figure 6. Flow chart of the fusion algorithm

下载: 全尺寸图片幻灯片

4. 仿真环境搭建

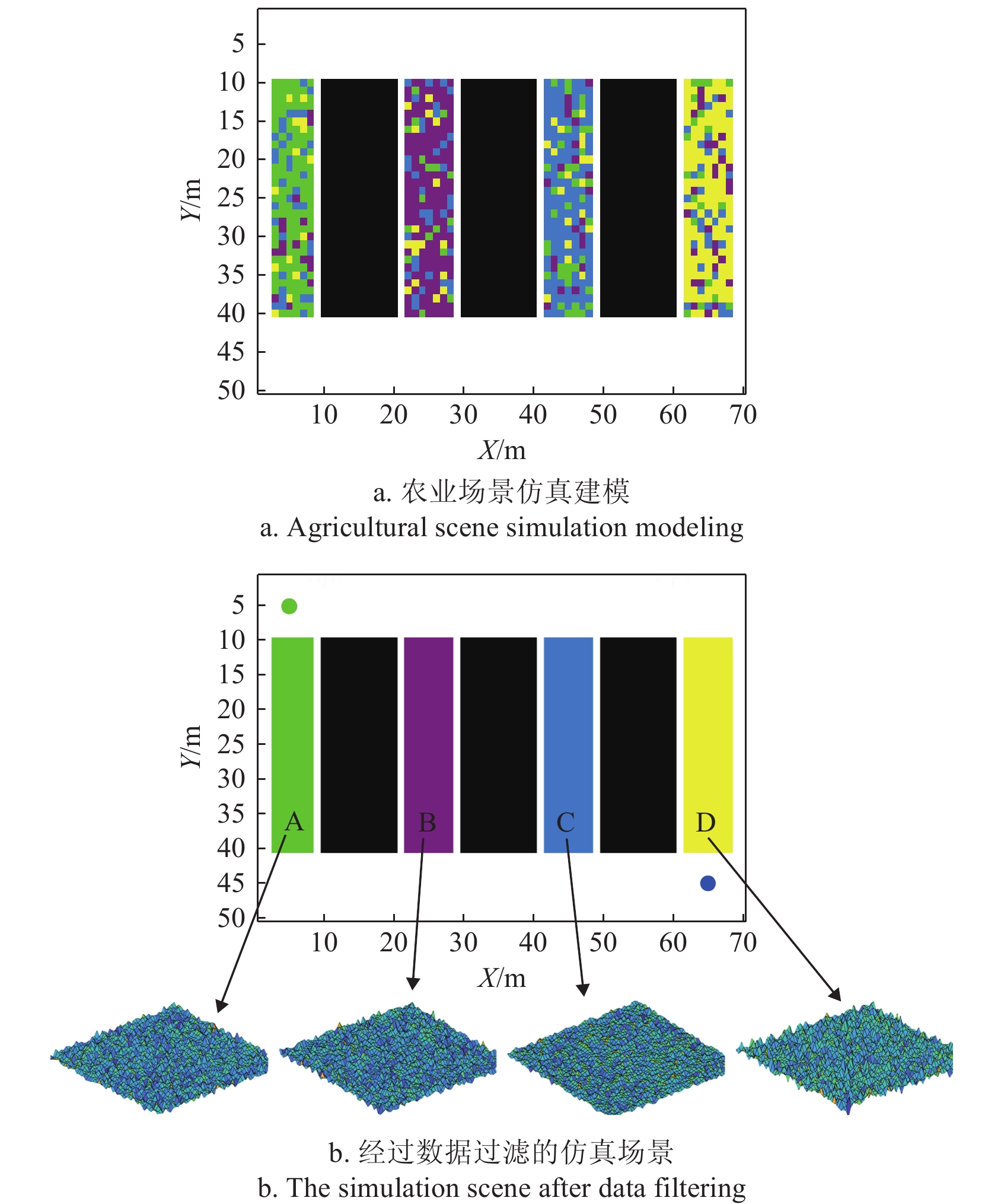
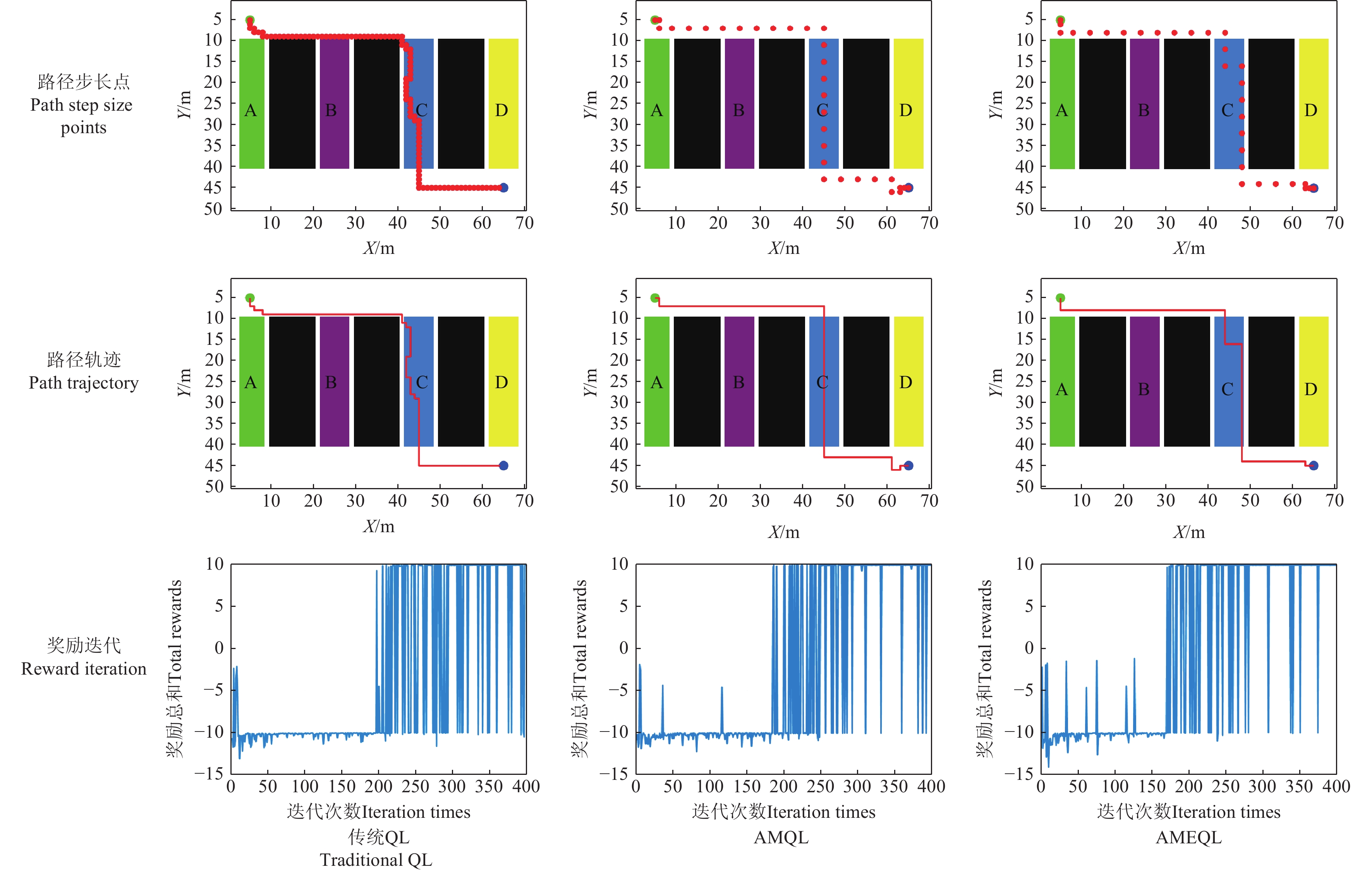
为了测试传统QL算法与优化QL算法的路径规划效果，本文在仿真试验中基于实际番茄温室农业场景进行了仿真建模，图7为农业环境实际取景，为仿真环境的搭建作参考。图8中的场景模拟采用70 m×50 m的栅格表示，包含3条垄道（种植区）与4条过道（工作区），其中垄道用黑色栅格表示，过道的数据通过IMU测量获得4种不同粗糙度的地面信息^[32]。

图 7 农业环境实际取景

Figure 7. Actual scene capture of the agricultural environment

下载: 全尺寸图片幻灯片

由于地形复杂，本文对IMU数据进行了滤波、去噪处理，仅保留4种粗糙度颜色（表2），白色区域表示无粗糙度地面。在仿真试验中，为了减少计算量，对图8中采集到的过道数据进行过滤处理，仅考虑影响最大的因素，其中“绿点”代表始点，“蓝点”代表终点，A～D为不同地面粗糙度，底盘在路径规划过程中，需要避免触碰垄道，并对地面粗糙度进行能量管理分析，使得强化学习算法在路径规划时自动权衡多种因素（如式（2）所示）以找到最优路径。

图 8 仿真环境搭建

注：图中A~D分别为表2中绿色、紫色、蓝色、黄色对应的粗糙度等级。

Figure 8. Simulation environment construction

Note: In the figure, A to D represent the roughness levels corresponding to green, purple, blue, and yellow in table 2.

下载: 全尺寸图片幻灯片

5. 仿真验证

为验证所提出方法的有效性，本文将试验分为3种：传统Q-Learning算法（QL）、基于自适应多步长的优化算法（AMQL）以及融合了AMQL与自适应变ε-greedy的优化算法（AEQL）的优化算法（AMEQL），用以实现对底盘的能量管理控制策略进行仿真测试。在仿真中，3种强化学习算法参数：学习率为0.1，折扣率为0.9，初始探索率为1，最小探索率为0.01，QL、AMQL算法的探索衰减率为0.99，AMEQL的探索衰减率采用式（5）-（8）计算获得；最大迭代次数为400，最大探索步数为300，QL的初始探索步长为1，AMQL、AMEQL的初始探索步长为自适应多步长。图9为3种算法在400次迭代之后的路径规划对比，其中包含所走的路径步长点（可观测其自适应步长变化）、训练输出最优路径以及3种算法的奖励迭代，图中“红色圆点”表示路径点，相邻路径点的距离表示步长，“红线”表示所走路径。由图可知，3种算法所走路径均为第三垄道，符合预期的分析。

图 9 3种试验方法在400次迭代之后的路径规划对比

Figure 9. Comparison of path planning after 400 iterations among the three experimental methods

下载: 全尺寸图片幻灯片

通过对传统QL算法、AMQL算法以及AMEQL算法进行对比分析可知：传统QL算法收敛速度慢，稳定性差，且拐点的数量较多，在300次迭代之后，奖励值波动仍旧较大，在实际进行路径规划时并不可取；相对于传统QL算法，AMQL的迭代速度提升相对明显，稳定性更强，在300次迭代之后，奖励值的波动相对有所降低；AMEQL算法的收敛速度最快，收敛效率最高，在迭代280次时，奖励值就趋于稳定，算法稳定性最高。

为了体现改进算法在解决问题方面的有效性，本文通过300轮仿真试验，其相关强化学习参数与分别对传统QL算法、AMQL算法和AMEQL算法在单垄道（30 m×20 m），双垄道（50 m×50 m）以及三垄道（70 m×50 m）下进行路径规划对比，如图10所示。

图 10 3种仿真环境

Figure 10. Three kinds of simulation environments

下载: 全尺寸图片幻灯片

数据结果如表3所示，在进行完整400次迭代时，在单垄道里面，AMQL算法相比于传统QL算法，训练平均时间降低4.21%，收敛平均迭代次数降低4.92%，路径平均拐点数降低66.67%，收敛后的平均波动次数减少20.83%；AMEQL算法迭代的平均时间最短，相比于传统QL算法，训练平均时间降低23.18%，收敛平均迭代次数降低42.16%，路径平均拐点数降低66.67%，收敛后的平均波动次数降低10.42%，到达最大奖励后每7.93次迭代波动1次，而AMQL每7.97次迭代波动1次。

表 3 3种算法仿真数据对比

Table 3. Comparison of simulation data of the three algorithms

垄道大小 Ridge size	收敛平均迭代次数 Convergence average number of iterations			训练平均使用时间 Average training usage time/s			路径平均拐点数 Average number of turning points on the path			收敛后的平均波动次数 Average number of fluctuations after convergence
垄道大小 Ridge size	QL	AMQL	AMEQL	QL	AMQL	AMEQL	QL	AMQL	AMEQL	QL	AMQL	AMEQL
单垄道	102	97	59	95	91	73	9	3	3	48	38	43
双垄道	157	136	129	169	114	108	11	5	3	46	41	38
三垄道	208	191	185	195	121	109	12	7	6	42	37	34

下载: 导出CSV

| 显示表格

在双垄道里面，AMQL算法相比于传统QL算法，训练平均时间降低32.54%，收敛平均迭代次数降低13.38%，路径平均拐点数降低54.54%，收敛后的平均波动次数减少10.87%；AMEQL算法相比于传统QL算法，训练平均时间降低36.09%，收敛平均迭代次数降低17.83%，路径平均拐点数降低72.73%，收敛后的平均波动次数降低17.39%，到达最大奖励后每7.13次迭代波动1次，而AMQL每6.43次迭代波动1次。

在三垄道里面，AMQL算法相比于传统QL算法，训练平均时间降低37.95%，收敛平均迭代次数降低8.17%，路径平均拐点数降低41.67%，收敛后的平均波动次数降低11.91%；AMEQL算法相比于传统QL算法，训练平均时间降低44.10%，收敛平均迭代次数降低11.06%，路径平均拐点数降低63.13%，收敛后的平均波动次数降低15.62%，到达最大奖励后每6.32次迭代波动1次，而AMQL每5.64次迭代波动1次。

通过对3种垄道的数据进行统计分析：AMQL相对于传统QL算法，训练平均时间降低23.74%，收敛平均迭代次数降低8.82%，路径平均拐点数降低54.29%，收敛后的平均波动次数降低14.54%；AMEQL相对于传统QL算法，训练平均时间降低34.46%，收敛平均迭代次数降低18.02%，路径平均拐点数降低63.13%，收敛后的平均波动次数减少15.62%，在400次迭代过程中，AMEQL到达最大奖励后平均每7.12次迭代波动1次，而AMQL平均每6.68次迭代波动1次。可知AMEQL训练时间最短，收敛最快，路径拐点数量最低，奖励波动最小，而AMQL次之。

6. 结　论

本文针对温室机器人底盘在行驶过程中地面粗糙度对电池寿命、利用率的影响以及传统路径规划、深度学习路径规划的问题，提出了基于先验知识构建分级预打分奖励模型的方法，并通过增加曼哈顿距离构建奖励函数，提高了电池寿命和利用率；同时，针对传统Q-Learning算法的迭代时间长、收敛效率低、易陷入局部最优及拐点多等问题，本文提出了自适应变步长的优化算法（adaptive multi-step Q-learning，AMQL）和基于自适应改变探索率的优化算法（adaptive ε -greedy Q-learning，AEQL），并将两者进行融合，提出了一种自适应多步长和变 ε -greedy融合算法（adaptive Multi-step and ε-greedy Q-learning，AMEQL），通过仿真对比的方式，验证了AMEQL与AMQL算法的性能表现。最后通过对3种垄道的数据进行数据统计。结果表明，AMEQL训练平均使用时间最短，收敛速度最快，路径平均拐点数缩减最多，训练效果最稳定，AMQL次之：

1）AMEQL相对于传统QL算法，训练平均时间降低34.46%，收敛平均迭代次数降低18.02%，路径平均拐点数降低63.13%，收敛后的平均波动次数减少15.62%；

2）AMQL相对于传统QL算法，训练平均时间降低23.74%，收敛平均迭代次数降低8.82%，路径平均拐点数降低54.29%，收敛后的平均波动次数降低14.54%；

3）在400次迭代过程中，AMEQL到达最大奖励后平均每7.12次迭代波动1次，而AMQL平均每6.68次迭代波动1次，可知AMEQL训练时间最短，收敛最快，路径拐点数量最低，奖励波动最小，而AMQL次之。

图 1 RBF神经网络结构图

注：x是输入变量；R是隐含层输出；ω是隐含层到输出层的连接权值；y是实际输出。

Figure 1. RBF neural network structure

Note: x is the input variable; R is the output of hidden layer; ω is the weight from hidden layer to output layer; y is the actual output.

下载: 全尺寸图片幻灯片

图 2 不同方法初始化种群对比

Figure 2. Comparison of different methods to initialize population

下载: 全尺寸图片幻灯片

图 3 拉普拉斯交叉密度函数(f(x))曲线

Figure 3. Laplace density function curve

下载: 全尺寸图片幻灯片

图 4 ICDO算法流程图

注：α、β和γ分别表示群体中最优解、次优解和第三优解；r₁、r₂为采用不同方式进行位置更新的随机数。

Figure 4. ICDO algorithm flow chart

Note: α, β and γ represent the optimal solution, sub-optimal solution and the third optimal solution in the population, respectively. r₁ and r₂ are random numbers that are updated in different ways.

下载: 全尺寸图片幻灯片

图 5 ICDO-RBFNN数据融合模型

注：ICDO为改进的切诺贝利灾难优化器；RBFNN为径向基函数神经网络。

Figure 5. ICDO-RBFNN data fusion model

Note: ICDO is improved Chernobyl disaster optimizer; RBFNN is radial basis function neural network.

下载: 全尺寸图片幻灯片

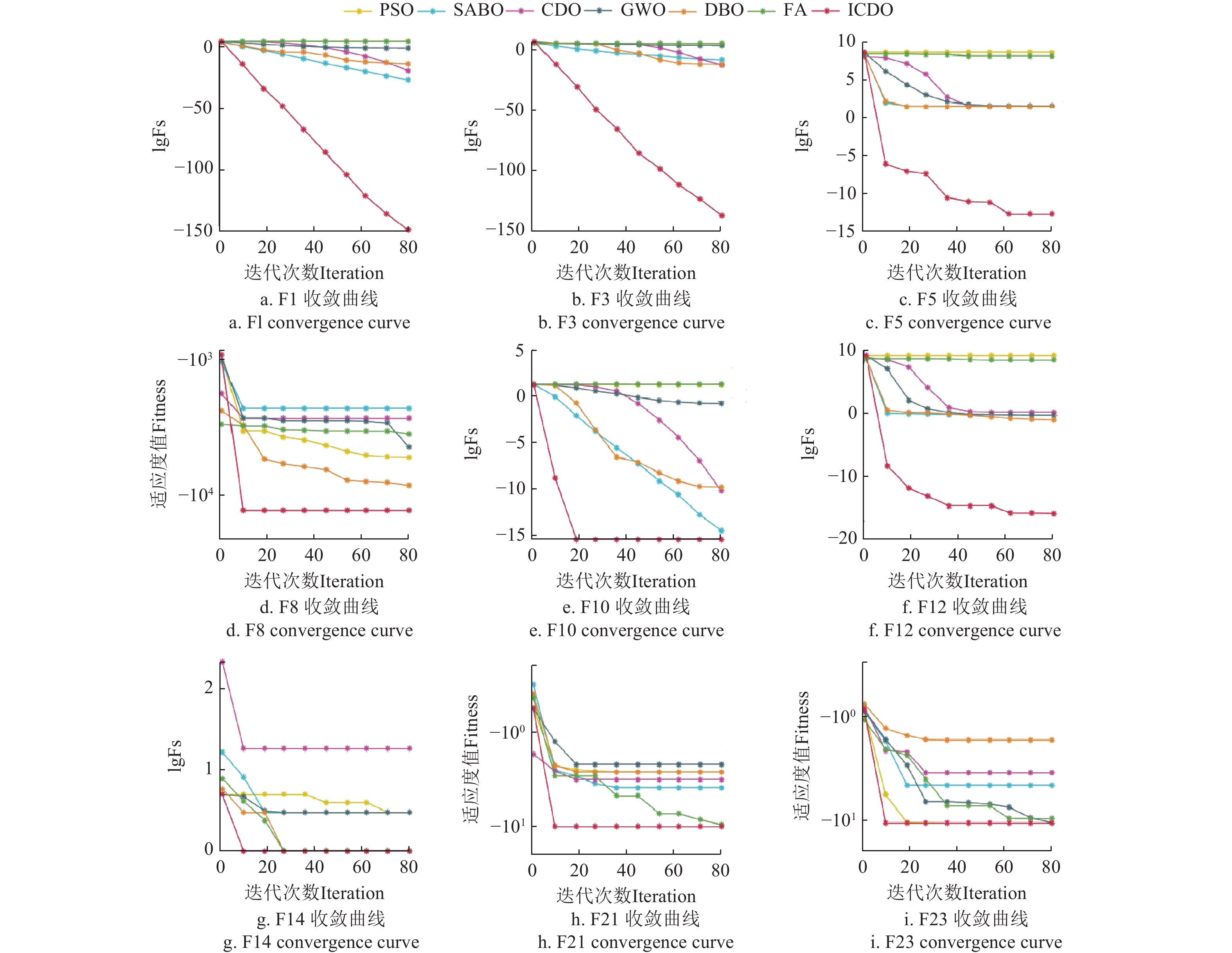
图 6 不同算法的收敛过程

注：CDO为切诺贝利灾难优化器；PSO为粒子群优化算法；GWO为灰狼优化算法；FA为萤火虫算法；DBO为蜣螂优化器算法； SABO为减法优化器；Fs为适应度值。

Figure 6. Convergence curve of different algorithms

Note: CDO is Chernobyl disaster optimizer; PSO is particle swarm optimization; GWO is grey wolf optimization; FA is firefly algorithm; DBO is dung beetle optimizer; SABO is subtraction average based optimizer; Fs is fitness.

下载: 全尺寸图片幻灯片

图 7 不同模型AQI融合的相对误差对比

Figure 7. Relative error comparison diagram of AQI fusion of different models

下载: 全尺寸图片幻灯片

图 8 温室环境等级融合对比

Figure 8. Comparison of greenhouse environment grade fusion

下载: 全尺寸图片幻灯片

表 1 基准函数

Table 1 Benchmark functions

函数 Function		维度 Dimensional	范围 Range	最优值 Optimal value
高维单峰函数	F1	30	[−100,100]	0
	F3	30	[−100,100]	0
	F5	30	[−100,100]	0
高维多峰函数	F8	30	[−500,500]	−418.9829×维度
	F10	30	[−32,32]	0
	F12	30	[−50,50]	0
固定维多峰函数	F14	2	[−65,65]	1
	F21	4	[0,10]	−10.1523
	F23	4	[0,10]	−10.5363

下载: 导出CSV

表 2 不同算法基准函数试验结果

Table 2 Benchmark functions experimental result

函数Function	指标Index	PSO	SABO	GWO	DBO	FA	CDO	ICDO
F1	方差	1.05E+00	1.68E-55	7.20E-03	7.22E-19	1.91E+07	1.04E-37	8.44E-263
	均值	6.00E+04	4.07E-28	1.29E-01	8.98E-11	4.88E+04	1.65E-19	9.80E-133
	最优值	6.00E+04	4.18E-30	1.60E-02	6.04E-34	3.56E+04	2.19E-20	3.48E-153
F3	方差	2.55E+06	3.88E-14	1.75E+04	3.57E-32	1.19E+08	2.42E-20	2.01E-269
	均值	3.74E+04	8.11E-07	4.29E+02	1.34E-16	5.59E+04	1.11E-10	3.18E-135
	最优值	3.63E+04	6.72E-07	3.35E+02	1.97E-20	4.82E+04	1.37E-12	7.09E-138
F5	方差	5.36E+08	1.28E-02	7.31E+00	2.68E-05	2.33E+14	2.27E-02	4.30E-27
	均值	4.00E+08	2.88E+01	3.12E+01	2.81E+01	1.35E+08	2.86E+01	4.93E-14
	最优值	4.00E+08	2.87E+01	2.93E+01	2.81E+01	1.24E+08	2.85E+01	2.96E-15
F8	方差	6.50E+05	1.13E+05	1.12E+06	4.19E+05	9.45E+04	2.33E+05	4.21E+05
	均值	−8.40E+03	−2.80E+03	−5.29E+03	−6.85E+03	−4.16E+03	−3.25E+03	−1.25E+04
	最优值	−9.69E+03	−3.45E+03	−4.51E+03	−6.82E+03	−8.69E+03	−4.86E+03	−1.26E+04
F10	方差	6.42E-07	1.10E-29	8.03E-01	2.57E-13	3.99E-02	2.22E-21	0.00E+00
	均值	1.90E+01	5.98E-15	5.70E-01	1.35E-07	2.01E+01	9.66E-11	8.88E-16
	最优值	1.90E+01	4.44E-15	6.83E-02	7.99E-15	1.95E+01	4.57E-11	8.88E-16
F12	方差	4.84E+00	1.39E-02	1.89E-01	1.40E-03	2.91E+15	1.02E-02	4.83E-30
	均值	1.54E+09	4.20E-01	5.00E-01	9.62E-02	2.54E+08	1.65E+00	1.19E-15
	最优值	1.54E+09	2.58E-01	6.93E-02	3.62E-02	1.41E+08	1.12E+00	1.09E-20
F14	方差	6.49E-01	7.97E+00	1.25E+00	1.26E+00	1.68E-01	2.01E+01	2.89E+00
	均值	2.59E+00	3.98E+00	3.01E+00	1.96E+00	1.26E+00	1.50E+01	4.03E+00
	最优值	9.98E-01	9.98E-01	9.98E-01	9.98E-01	9.98E-01	2.02E+00	9.98E-01
F21	方差	1.39E+01	1.11E+00	7.08E+00	8.06E+00	2.02E+00	1.04E+00	4.81E+00
	均值	−7.17E+00	−3.84E+00	−8.93E+00	−6.24E+00	−8.99E+00	−3.81E+00	−8.96E+00
	最优值	−1.02E+01	−5.04E+00	−6.07E+00	−1.01E+01	−1.02E+01	−1.01E+01	−1.02E+01
F23	方差	9.73E+00	1.19E+00	3.28E+00	1.30E+01	1.08E-01	1.58E+00	6.72E+00
	均值	−9.00E+00	−3.70E+00	−9.99E+00	−6.96E+00	−9.80E+00	−4.43E+00	−8.73E+00
	最优值	−1.05E+01	−8.27E+00	−8.71E+00	−1.05E+01	−1.05E+01	−1.04E+01	−1.05E+01

下载: 导出CSV

表 3 AQI融合对比分析

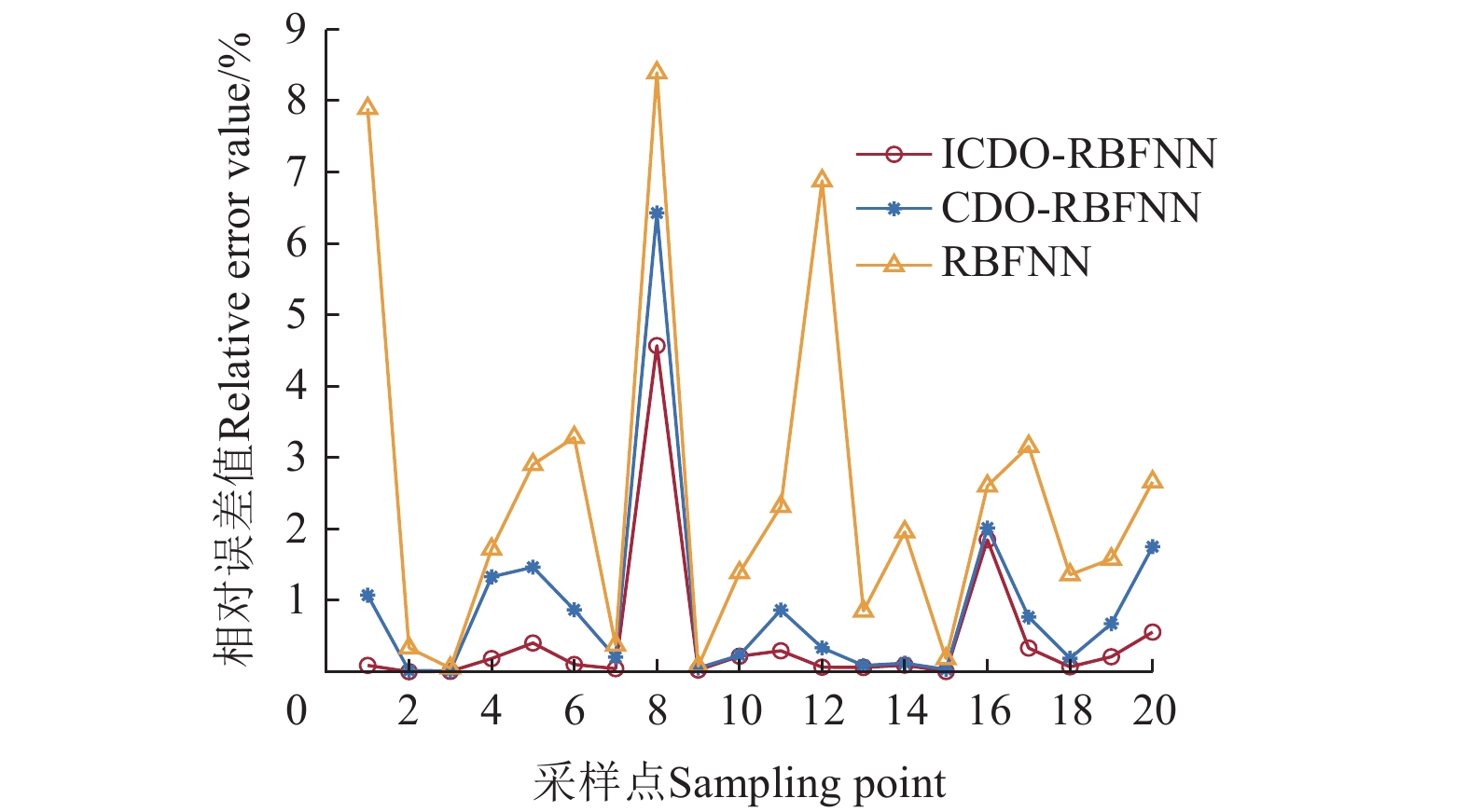
Table 3 AQI fusion comparative analysis

模型Model	R²	均方误差 Mean square error	平均绝对百分比误差 Mean absolute percentage error/%	平均耗时Average time consumption/s
BPNN融合算法	0.936	49.133	9.562	0.75
GA-BPNN融合算法	0.948	25.635	10.096	4.75
Elman神经网络融合算法	0.910	41.282	8.042	0.13
RBFNN融合算法	0.988	5.598	2.060	0.04
CDO-RBFNN融合算法	0.998	0.803	1.029	8.60
ICDO-RBFNN融合算法	0.999	0.348	0.729	8.99

下载: 导出CSV

表 4 农业温室环境等级划分

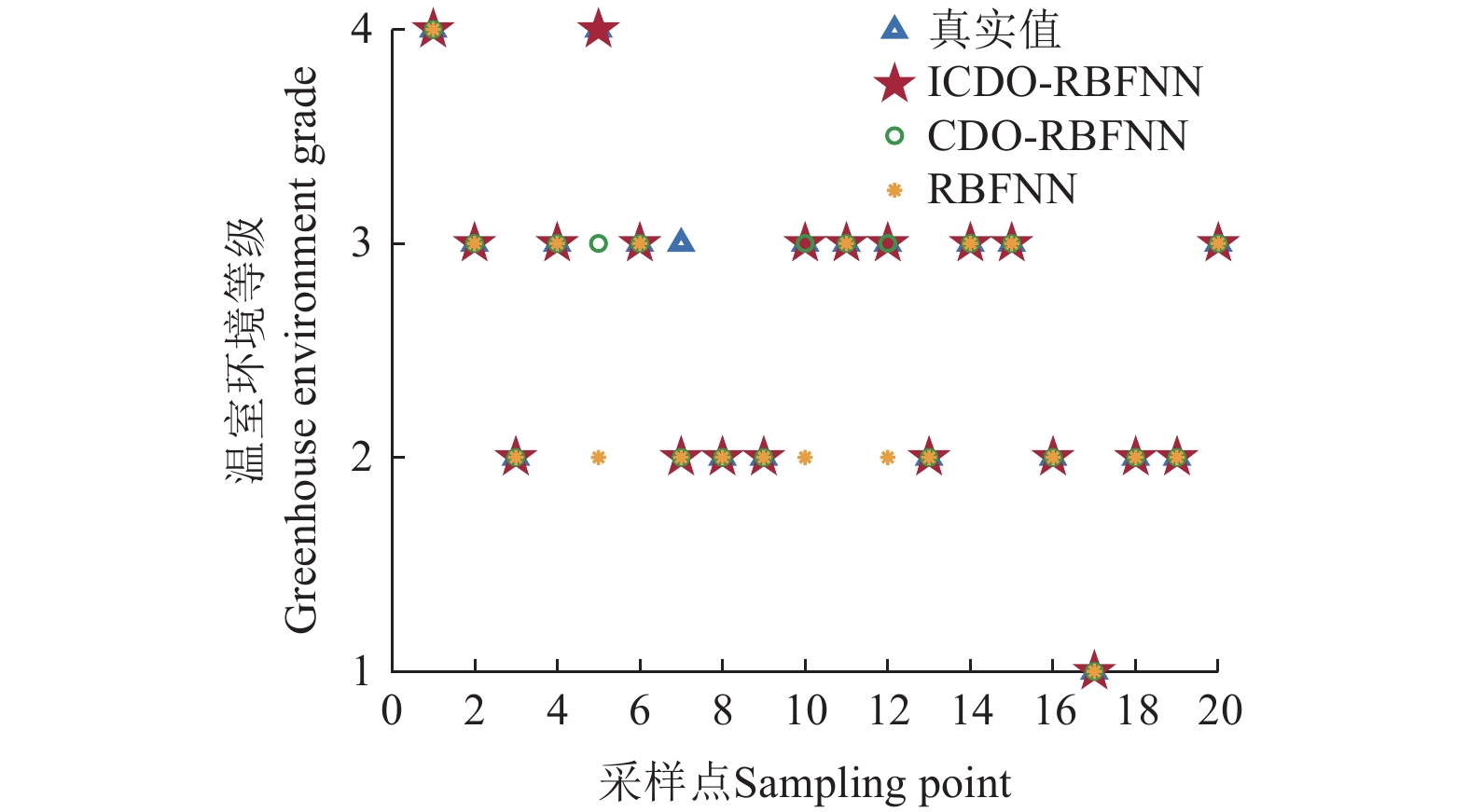
Table 4 Greenhouse environment classification

温度Temperature（t）/℃	湿度Relative humidity(RH)/%	等级Level
26≤t≤28	50≤RH≤70	4（最佳生长环境）
20≤t<26; 28<t≤30	40≤RH<50; 70<RH≤80	3（生长环境）
5≤t<20;30<t≤35	40≤RH<50; 70<RH≤80	2（存活环境）
t < 5; t >35	40>RH; RH>80	1（恶劣环境）

下载: 导出CSV

表 5 温室环境等级融合对比分析

Table 5 Comparative analysis of greenhouse environment grade fusion

模型 Model	准确率 Accuracy/%	精准率 Precision/%	平均耗时Average time consumption/s
BPNN融合算法	46.46	63.44	0.04
GA-BPNN融合算法	99.20	98.93	7.75
Elman神经网络融合算法	76.37	95.59	0.25
RBFNN融合算法	94.49	92.93	0.22
CDO-RBFNN融合算法	96.85	96.81	4.65
ICDO-RBFNN融合算法	99.21	99.91	4.86

下载: 导出CSV

参考文献(27)

[1]	WANG J, WU Z, LIANG Y, et al. Perception methods for adverse weather based on vehicle infrastructure cooperation system: a review[J]. Sensors, 2024, 24(2): 374. doi: 10.3390/s24020374
[2]	张柏,凌彩金,李露青,等. 基于数据融合策略的红茶发酵程度判别[J]. 农业工程学报,2022,38(15):339-347. doi: 10.11975/j.issn.1002-6819.2022.15.037 ZHANG Bai, LING Caijin, LI Luqing, et al. Discrimination of black tea fermentation degrees based on data fusion strategy[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2022, 38(15): 339-347. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.2022.15.037
[3]	匡亮,施珮,季云峰,等. 改进型支持度函数的WSN水质监测数据融合方法[J]. 农业工程学报,2020,36(16):192-200. doi: 10.11975/j.issn.1002-6819.2020.16.024 KUANG Liang, SHI Pei, JI Yunfeng, et al. Data fusion method for water quality monitoring using WSN based on improved support function[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2020, 36(16): 192-200. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.2020.16.024
[4]	SONG J H, SHI X Y, WANG H J, et al. Combination of feature selection and geographical stratification increases the soil total nitrogen estimation[J]. Computers and Electronics in Agriculture, 2024, 218: 108636. doi: 10.1016/j.compag.2024.108636
[5]	杜肖鹏,李恺,王春辉,等. 国内温室空气温湿度检测及传输技术研究进展[J]. 农业工程技术,2022,42(34):28-34.
[6]	曾喆昭,王耀南. 基于正交基神经网络算法的多传感器数据融合方法[J]. 传感技术学报,2007(6):1368-1370. doi: 10.3969/j.issn.1004-1699.2007.06.038 ZENG Zhezhao, WANG Yaonan. Multi-sensor information fusion approach based on the basis neural network algorithm with orthogonal basis functions[J]. Chinese Journal of Sensors and Actuators, 2007(6): 1368-1370. (in Chinese with English abstract) doi: 10.3969/j.issn.1004-1699.2007.06.038
[7]	杜昭,张文榕,朱兴一. 基于网联车辆数据融合的路面平整度评估方法[J]. 中国公路学报,2024,37(6):302-316. DU Zhao, ZHANG Wenrong, ZHU Xingyi. Road roughness assessment based on fusion of connected-vehicles data[J]. China Journal of Highway and Transport, 2024, 37(6): 302-316. (in Chinese with English abstract)
[8]	杨华,陈树生,高正红,等. 基于贝叶斯框架的旋翼气动力数据融合[J]. 航空学报,2024,45(8):138-150. YANG Hua, CHEN Shusheng, GAO Zhenghong, et al. Research on rotor aerodynamic data fusion based on bayesian frame-work[J]. Acta Aeronautica et Astronautica Sinica, 2024, 45(8): 138-150. (in Chinese with English abstract)
[9]	XIAO H. Computer technology of multisensor data fusion based on FWA–BP network[J]. Journal of Intelligent Systems, 2023, 32(1): 6099-6108. doi: 10.1515/jisys-2022-0278
[10]	DONG Y, LIU P X, YUE X J, et al. Data fusion algorithm based on classification adaptive estimation weighted fusion in WSN[J]. Wireless Personal Communications, 2022, 127(4): 2859-2871. doi: 10.1007/s11277-022-09900-x
[11]	ANNARITA D, ALBERTO R, FRANCESCO P L, et al. DAFNE: A matlab toolbox for Bayesian multi-source remote sensing and ancillary data fusion, with application to flood mapping[J]. Computers & Geosciences, 2018, 112: 64-75.
[12]	LIU H B, FANG S Y, JI J H. An improved weighted fusion algorithm of multi-sensor[J]. Journal of Physics: Conference Series, 2020, 1453(1): 012009.
[13]	WU L S, CHEN L, HAO X R. Multi-sensor data fusion algorithm for indoor fire early warning based on BP neural network[J]. Information, 2021, 12(2): 59-59. doi: 10.3390/info12020059
[14]	吴晟,闫娇娇,张晶. 基于启发式萤火虫的BP神经网络数据融合算法[J]. 传感器与微系统,2021,40(4):146-149, 156. WU Sheng, YAN Jiaojiao, ZHANG Jing. BPNN data fusion algorithm based on heuristic firefly[J]. Transducer and Microsystem Technologies, 2021, 40(4): 146-149, 156. (in Chinese with English abstract)
[15]	IMANE E N H, ALLEL H, MOHAND L. Multisensor data fusion in IoT environments in dempster-shafer theory setting: An improved evidence distance-based approach[J]. Sensors (Basel, Switzerland), 2023, 23(11): 5141. doi: 10.3390/s23115141
[16]	张志勇,路小娟,孔令刚,等. K-means结合RBF神经网络预测线性菲涅尔集热回路出口熔盐温度[J]. 农业工程学报,2021,37(3):213-222. ZHANG Zhiyong, LU Xiaojuan, KONG Linggang, et al. Predicting molten salt temperature at the circuit outlet of Linear Fresnelheat collector using K-means combined with RBF neural network[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2021, 37(3): 213-222. (in Chinese with English abstract)
[17]	SHEHADEH H A. Chernobyl disaster optimizer (CDO): A novel meta-heuristic method for global optimization[J]. Neural Computing and Applications, 2023, 35(15): 10733-10749.
[18]	闫少强,杨萍,朱东林,等. 基于佳点集的改进麻雀搜索算法[J]. 北京航空航天大学学报,2023,49(10):2790-2798. YAN Shaoqiang, YANG Ping, ZHU Donglin, et al. Improved sparrow search algorithm based on good point set[J]. Journal of Beijing University of Aeronautics and Astronautics, 2023, 49(10): 2790-2798. (in Chinese with English abstract)
[19]	WANG M H, MA Y J. A differential evolution algorithm based on accompanying population and piecewise evolution strategy[J]. Applied Soft Computing Journal, 2023, 143: 110390. doi: 10.1016/j.asoc.2023.110390
[20]	YU H L, QIAO S M, ALI A H, et al. Laplace crossover and random replacement strategy boosted Harris hawks optimization: Performance optimization and analysis[J]. Journal of Computational Design and Engineering, 2022, 9(5): 1879-1916. doi: 10.1093/jcde/qwac085
[21]	YANG Z L, MOURSHED M, LIU K L, et al. A novel competitive swarm optimized RBF neural network model for short-term solar power generation forecasting[J]. Neurocomputing, 2020, 397: 415-421. doi: 10.1016/j.neucom.2019.09.110
[22]	ZHENG X P, NIE B, CHEN J D, et al. An improved particle swarm optimization combined with double-chaos search[J]. Mathematical Biosciences and Engineering: MBE, 2023, 20(9): 15737-15764. doi: 10.3934/mbe.2023701
[23]	MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software, 2014, 69: 46-61. doi: 10.1016/j.advengsoft.2013.12.007
[24]	TILAHUN L S , NGNOTCHOUYE T M J . Firefly algorithm for discrete optimization problems: A survey[J]. KSCE Journal of Civil Engineering, 2017, 21(2): 535-545.
[25]	XUE J, SHEN B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization[J]. The Journal of Supercomputing, 2023, 79(7): 7305-7336. doi: 10.1007/s11227-022-04959-6
[26]	PAVEL T, MOHAMMAD D. Subtraction-average-based optimizer: A new swarm-inspired metaheuristic algorithm for solving optimization problems[J]. Biomimetics (Basel, Switzerland), 2023, 8(2): 2313-7673.
[27]	潘劲成,李少波,周鹏,等. 改进正弦算法引导的蜣螂优化算法[J]. 计算机工程与应用,2023,59(22):92-110. PAN Jincheng, Ll Shaobo, ZHOU Peng, et al. Dung beetle optimization algorithm guided by improved sine algorithm[J]. Computer Engineering and Applications, 2023, 59(22): 92-110. (in Chinese with English abstract)

施引文献(2)

期刊类型引用(2)

1.	蒋丙婷，李如蕊，方越，郑文杰，周莹，李能波，何霞红，王振兴. 乳酸菌发酵对铁皮石斛抗氧化活性和酚类化合物的影响. 农业工程学报. 2025(02): 328-337 . 本站查看
2.	林平冬，向韩，岳稳，刘景，陈鑫珠. 栀子多糖的提取纯化及其体外抗氧化活性研究. 农业工程学报. 2025(03): 309-317 . 本站查看