基于数据-物理混合模型的菇房空调节能控制方法

孔祥书; 郑文刚; 张馨; 王明飞; 单飞飞; 赵倩

doi:10.11975/j.issn.1002-6819.202410017

基于数据-物理混合模型的菇房空调节能控制方法

孔祥书^1,,
郑文刚^{1, 2},
张馨^{1, 2},
王明飞^{1, 2, ,},
单飞飞^{1, 2},
赵倩^{1, 2}

1.
北京市农林科学院智能装备技术研究中心，北京 100097
2.
北京市农林科学院信息技术研究中心，北京 100097

基金项目: 国家现代农业产业技术体系项目（CARS-20）；北京市食用菌创新团队项目（BAIC03-2024）

详细信息

作者简介:
孔祥书，研究方向为食用菌工厂化智能管控。Email：kongxs@nercita.org.cn

通讯作者:
王明飞，高级工程师，研究方向为食用菌智能检测与控制技术。Email：Wangmf@nercita.org.cn

中图分类号: S24
计量
- 文章访问数: 0
- HTML全文浏览量: 0
- PDF下载量: 0
出版历程
- 收稿日期: 2024-10-04
- 修回日期: 2024-12-23
- 网络出版日期: 2025-01-02
- 刊出日期: 2025-02-27

Energy-saving control method of air conditioning in mushroom house based on data - physics mixed model

KONG Xiangshu^1,,
ZHENG Wengang^{1, 2},
ZHANG Xin^{1, 2},
WANG Mingfei^{1, 2, ,},
SHAN Feifei^{1, 2},
ZHAO Qian^{1, 2}

1.
Intelligent Equipment Technology Research Center, Beijing Academy of Agriculture and Forestry Sciences, Beijing 100097, China
2.
Information Technology Research Center, Beijing Academy of Agriculture and Forestry Sciences, Beijing 100097, China

摘要

摘要:
针对模型预测控制在菇房节能控制中存在纯数据驱动温度预测模型可解释性差、优化求解速度慢等问题，该研究提出了一种基于数据-物理混合模型的菇房空调节能控制方法。首先，使用门控循环单元神经网络（gated recurrent unit neural network, GRU）与注意力机制（attention）作为预测模型，将菇房内部热平衡方程纳入损失函数中，实现基于数据-物理混合模型的菇房温度预测方法。然后，基于模型输出与参考轨迹的偏离程度和设备控制量建立目标函数。最后，利用改进型Adam算法快速地求解出空调在控制时域内的最优控制序列，实现菇房空调能耗最优控制。试验结果表明：与纯数据驱动的GRU模型相比，本文所提出的菇房温度预测模型，预测精度提高18%，均方根误差可控制在0.10 ℃内。与自适应矩估计（adaptive moment estimation，Adam）优化算法相比，改进型Adam算法适应度值降低6%，与带精英策略的快速非支配排序遗传算法相比（non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ）运算时长减少81%。与传统的阈值控制方法相比，本文所提出的模型预测控制方法跟踪精度提高63%，控制精度的均方根误差平均降低了73%，空调能耗平均降低了12%。该研究为菇房空调的节能控制提供了有效的控制方法。
- 节能 /
- 模型预测控制 /
- 深度学习 /
- 数据-物理混合驱动模型 /
- 菇房
Abstract:
The data-driven model predictive control (MPC) has been widely applied in the field of energy-saving control. However, the low interpretability and speed of optimization often occur on the pure MPC of temperature in the energy-saving control system. In this study, a data-physics mixed model was proposed for the air conditioning energy-saving control system in mushroom houses. Firstly, a basic prediction model was established to combine the gated recurrent unit (GRU) neural network with the attention mechanism. Some influencing factors were considered, such as heat transfer from fresh air, heat dissipation from mushroom respiration, radiant heat from envelope structures, and air conditioning cooling. The internal thermal balance equation of the mushroom house was incorporated into the physical loss term, along with the data loss term between the predicted and actual temperatures. The loss function was then formed. The prediction model and the loss function together formed a special gray-box prediction model. Temperature prediction was implemented on the mushroom house using a data-physical hybrid model. Then, a target function was established to consider the deviation among the predicted temperature. The reference trajectory was taken as the prediction accuracy term, while the air conditioning operation time was taken as the energy consumption term. Finally, an improved Adam algorithm was developed to integrate the "belief" and the "look-ahead" mechanisms, according to the basic Adam algorithm. The target function was rapidly obtained in the optimal control sequence for the air conditioner over the control time domain. The first control value in the sequence was applied to the air conditioning system. Thus the optimal control was achieved to simultaneously consider both accuracy and energy consumption for the air conditioning system in the mushroom house. Experimental results showed that the temperature prediction model with the data-physical hybrid outperformed the various previous models. The accuracy of prediction was improved by 18%, compared with the pure data-driven GRU model, while the root mean square error (RMSE) was controlled within 0.10 °C, and the model training time was only 16 s. The fitness value of the improved Adam algorithm was 0.751, with a computation time of 47 s. A comparative analysis with various optimization algorithms showed that the fitness value decreased by 6%, compared with the Adam optimization algorithm, while the computation time was reduced by 81%, compared with the elitist fast non-dominated sorting genetic algorithm (NSGA-II). Compared with the traditional threshold control, the air conditioning model adapted the best to the flexible changes in the reference trajectory. The control input was adjusted in advance using a unique prediction mechanism, indicating the better tracking performance of the reference trajectory. The tracking accuracy was improved by 63% during a 5-day simulation experiment. The control accuracy RMSE was reduced by an average of 73% and the energy consumption of air conditioning was reduced by an average of 12%. The energy-saving control model enhanced the interpretability of the prediction. The computation speed was also improved with the high solution accuracy of the rolling optimization. The high robustness was used to change the control parameters. As such, precise temperature and energy-saving control were achieved in the mushroom house. The finding can also provide a strong reference for the energy-saving control system in industrialized mushroom cultivation.
- energy conservation /
- model predictive control /
- deep learning /
- data-physics hybrid driving model /
- mushroom room

HTML全文

0. 引　言

食用菌的工厂化生产模式不受天气、季节等自然因素约束，在精准可控环境下实现高效优质生产，因此其占比逐年增加^[1]。空调系统是实现养菌、出菇环境精准控制的必要条件^[2]。据统计，用于环境调控成本达到食用菌工厂能源消耗总成本的40%^[3]。空调能源消耗高已成为阻碍食用菌工厂化企业发展的核心问题之一。现有的菇房温度以阈值控制为主^[4]，在实际应用中存在温度波动大、能源消耗高等问题。比例-积分-微分（proportional-integral-derivative, PID）控制^[5]、强化学习^[6]与模型预测控制（model predictive control, MPC）^[7]等算法被应用于空调节能控制中。PID控制通过动态反馈调节控制行为，内部参数固定或预先确定，对外界环境变化的适应性较差^[8]；强化学习在复杂环境中需要大量数据、训练时间以及试错过程，因此不满足实时控制要求^[9]；而MPC利用预测模型推测系统未来行为，并在给定约束下，优化特定性能指标^[10]，已在设施农业上得到广泛研究^[11-12]。

MPC方法中的温度预测模型可分为白盒模型、黑盒模型与灰盒模型。白盒模型主要依赖建筑能源仿真程序，如EnergyPlus^[13]、TRNSYS^[14]与Modelica^[15]。这些模型由建筑系统内部传热机制推导而来，具有很强的可解释性。然而，在应用过程中它们对中间软件的发展高度依赖，需要一些如楼宇控制虚拟试验台之类的中间程序，将EnergyPlus等建筑能源仿真程序与Python或MATLAB等数据处理程序耦合，增加了使用的复杂性^[16-17]。黑盒模型以机器学习为主，能够在高维数据空间中找到复杂的模式或规律，多种模型被应用于建筑物的MPC中^[18-19]，其中长短期记忆神经网络（long short term memory, LSTM）及其衍生结构表现出了良好的预测效果^[20-22]。但此类数据驱动模型在数据拟合中缺乏可解释性，依赖于高质量数据，因此需要额外的物理规律对机器学习的拟合过程进行约束，进而提高预测精度^[23]。灰盒模型在建筑中使用较多的为等效阻容模型^[24]，主要难点在于物理参数的选择以及相关数据的获取^[25]。近年来，通过引入物理学的先验知识，来改进和优化机器学习模型的性能，不仅能提高数据效率，预测结果也更符合物理原理，可解释性更高^[26]。

另外，基于神经网络的MPC求解速度是制约规模化应用的重要问题之一。MPC需要同时考虑未来几个控制周期的最优控制量，导致其计算量远高于阈值控制与PID控制。最为普遍的两种求解方法是二次规划^[27-28]与智能优化算法^[29-30]。此两种方法都不可避免的增加了计算量，不适合较短控制周期内的连续在线求解。梯度下降算法（gradient descent algorithm, GD）作为多种优化算法的底层逻辑，在MPC控制中也有应用先例^[31]。自适应矩估计（adaptive moment estimation, Adam）算法以梯度下降算法为基础，结合动量与自适应学习率，在深度学习模型求解优化上得到了很好的应用^[32]。但Adam算法存在不收敛的情况，且在“大梯度、小曲率”的情况下收敛速度较慢^[33]。

综上所述，现有融合深度神经网络的MPC方法存在预测模型缺乏可解释性与实时性差两个问题，本文提出一种基于数据-物理混合模型的菇房空调节能控制方法，旨在用可快速求解的MPC方法，解决食用菌出菇房室内温度波动大、能源消耗高的问题。一方面，研究融合物理约束的深度神经网络预测模型，以门控循环单元神经网络（gated recurrent unit neural network, GRU）配合注意力机制（attention）作为基础预测模型，并在预测模型损失函数中添加菇房室内热平衡的物理约束，形成数据-物理混合温度预测模型。另一方面，提出一种融合AdaBelief算法与Nesterov算法的改进型Adam算法，缩短MPC控制周期的求解时间，为连续的在线优化求解提供技术支撑。最后，通过仿真试验和对比分析验证本文控制方法的可行性与有效性。

1. 方法与材料

1.1 菇房控制系统建模

MPC作为智能控制算法，使用预测模型来预知被控系统未来状态，并计算出在给定约束条件下的最优控制量。菇房温度自动控制系统可表示为

${t_{in}}(k + 1) = f({T_{in}}(k),D(k),U(k + 1))$

(1)

式中T_in为菇房室内温度t_in组成的温度序列，T_in(k)=[t_in(k), t_in(k-1),…, t_in(k-N₁)]，℃；U为控制动作u组成的控制序列，U(k+1)=[u(k+1), u(k),…,u(k+1-N₁)]；D为其余影响因素d组成的序列，D(k)=[d(k), d(k-1),…,d(k-N₁)]；k为周期数；N₁为预测步长；f(·)表示被控系统的状态函数，可表达为预测模型。

1.2 基于数据-物理混合模型的温度预测方法

由式（1）可知预测模型f(·)是实现模型预测控制的基础，与传统机器学习相比，LSTM通过设置遗忘门、输入门与输出门3种结构，解决了输入信息的保留、遗忘以及输出。GRU为LSTM网络的变体，仅有更新门和重置门组成^[34]。相较于LSTM，GRU结构更为简单、计算速度更快，具有优越的时序数据预测能力^[35]。其内部神经元结构如图1所示。

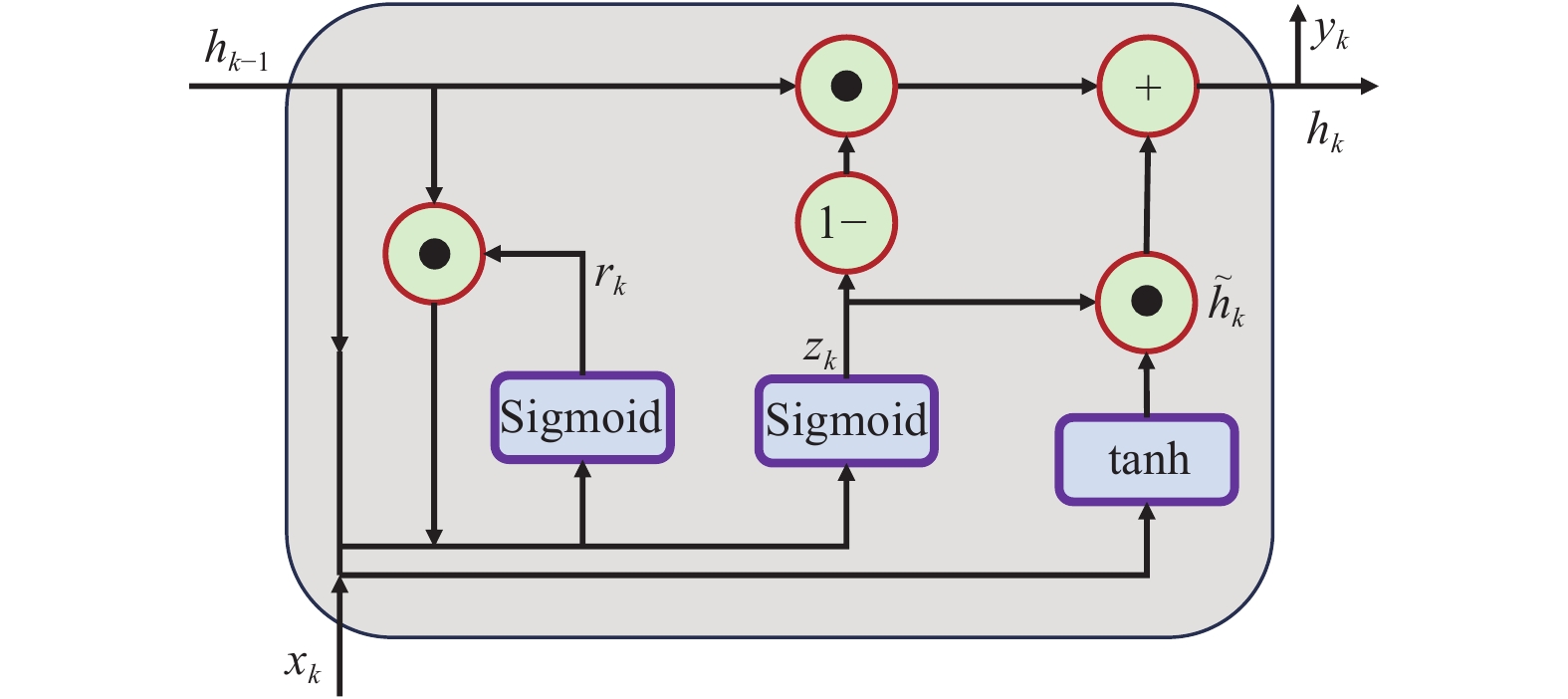
图 1 GRU神经元结构

注：x_k为输入；h_k-1为k-1周期的隐藏状态；y_k为输出；h_k为隐藏状态； r_k为重置门；z_k为更新门；

${\tilde h_k}$ 为候选隐藏状态；Sigmoid、tanh为激活函数，下同。

Figure 1. Gated recurrent unit（GRU）neuron structure

Note: x_k is the input; h_k-1 is the hidden state of the k-1 period; y_k is the output; h_k is the hidden state; r_k is the reset gate; z_k is the update gate;

${\tilde h_k}$ is the candidate hidden state; Sigmoid and tanh are activation functions, the same below.

下载: 全尺寸图片幻灯片

GRU神经元计算式为

$r_k=\mathrm{sigmoid}({{\boldsymbol{w_r}}}\times[x_k,h_{k-1}])$

(2)

${\textit{z}}_k=\mathrm{sigmoid}({\boldsymbol{w_z}}\times[x_k,h_{k-1}]))$

(3)

${\widetilde h_k} = \tanh ({{\boldsymbol{w_h}}} \times [{x_k},{r_k} \odot {h_{k - 1}}])$

(4)

${h_k} = {{\textit{z}}_k} \odot {h_{k - 1}} + (1 - {{\textit{z}}_k}) \odot {\widetilde h_k}$

(5)

式中w_r、w_z、w_h为参数矩阵；☉为Hadamard product（哈达玛积），即对应元素相乘。

此外注意力机制被证明可以有效提高深度学习模型的预测效果^[36]，因此本文将GRU与点积形式的注意力机制结合进行预测，其计算式为

${y}_{Att}=\mathrm{softmax}(g({\boldsymbol{Q}}\cdot {\boldsymbol{K}}))\cdot {\boldsymbol{V}}$

(6)

式中y_Att为注意力机制的输出信息；Q、K、V为注意力机制中的Key、Value、Query矩阵，均由GRU网络的输出y_k线性变化而来；g(·)为相似度计算式，由点积法计算得出；softmax为激活函数。

由上述式（2）～（6）可知，GRU-Attention网络为单纯的数据驱动模型，为提高模型的预测精度与泛化能力，本文将菇房内部热平衡以损失函数的形式参与到模型训练中。引发菇房内部热量变化路径有：

1）菇房内环境通过围护结构与外界环境产生热交换；

2）菌菇生长呼吸作用产热；

3）空调的供冷/热；

4）通过新风与室外交换的热量；

5）通过门缝逸散量与灯光等交换的热量。

菇房单个周期的热平衡方程如式（7）所示。

$\begin{split} \Delta {Q_{in}} =\;& \Delta {Q_{envelope}} + \Delta {Q_{fungus}} + \\ \;&\Delta {Q_{AC}} + \Delta {Q_{fersh - air}} + \Delta {Q_{other}} \end{split}$

(7)

式中ΔQ_in是室内总热量的变化，J；ΔQ_envelope是外界环境经围护结构传递到室内的热量，J；ΔQ_fungus是室内食用菌呼吸产生的热量，J；ΔQ_AC是空调制冷量，J；ΔQ_fresh-air是新风带来的热量，J；ΔQ_other是通过门缝逸散量和灯光等带来的室内热量，J。

由于菇房维护结构为全封闭式，外界环境通过太阳辐射将热量作用至围护结构，因此ΔQ_envelope计算式为

$\Delta {Q_{envelope}} = \Delta R \times A$

(8)

式中ΔR为室外太阳辐射变化量，W/m²；A为菇房受热表面积，m²；

食用菌呼吸过程进行葡萄糖的有氧分解时，能量利用率约为40%^[37]，其余能量以热能形式释放。通过食用菌一个生长周期内室内二氧化碳浓度变化平均值计算得出ΔQ_fungus。

空调制冷量ΔQ_AC计算式为

$\Delta {Q_{AC}} = \Delta u \times P$

(9)

式中Δu是控制量的变化量（空调开启时长，min），P是空调系统的输出功率，W。

ΔQ_fresh-air计算式为

$\Delta {Q_{fresh - air}} = ({t_{out}} - {t_{in}}) \times {V_{fresh - air}} \times \rho \times C$

(10)

式中t_out表示室外空气温度，℃；t_in表示室内温度，℃；V_fresh-air表示菇房换气的体积，m³；ρ表示空气密度，kg/m³；C表示空气比热容，kJ/(kg·℃)。

通过门缝逸散的热量与灯光散发的热量相对较少，因此Q_other可忽略不计。

将菇房室内热量变化ΔQ_in以温度变化的形式表达，其计算式为

$\Delta {Q_{in}} = ({t_{in - phy}}(k) - {t_{in}}(k - 1)) \times {m_{air}} \times C$

(11)

式中t_in-phy为经物理规则计算而出的室内温度，℃；m_air为菇房内空气质量，kg。

将式（8）～（11）带入至式（7）中可求出t_in-phy，设计基于物理规则的损失函数Loss_PHY，其计算式为

$Los{s_{PHY}} = \left| {{t_{in - phy}}(k) - {t_{in}}(k)} \right|$

(12)

除物理约束外，预测模型的损失函数还包括数据损失项，利用平均绝对误差（mean absolute error, MAE）作为评价指标，因此总的约束为

$Los{s_{total}} = Los{s_{MAE}} + Los{s_{PHY}}$

(13)

式中Loss_toatl为温度预测模型总的损失函数；Loss_MAE为温度预测模型中数据损失函数。

1.3 优化求解方法

1.3.1 优化求解目标

MPC通过求解目标函数得到控制时域内的最优控制量。本文满足食用菌最佳农艺条件下生长温度范围的同时，期望空调开启时长最短，基于系统输出与参考轨迹的偏离程度和空调设备的控制量建立目标函数j(k)，其计算式为

$\begin{split} j(k) = \;& min[{\sigma _2}{U^{mpc}}{(k)^2} + \\ \;& {\sigma _1}{({T_{in - C}}(k + 1) - {T_{in - pre}}(k + 1))^2}] \end{split}$

(14)

式中U^mpc为经MPC优化后的控制序列，U^mpc(k)=[u^mpc(k), u^mpc(k+1),…,u^mpc(k+N₂-1)]，u^mpc(k)表示第k周期下经MPC优化后的控制量；T_in-C为是室内温度参考轨迹序列T_in-C(k+1)=[t_in-C(k+1), t_in-C(k+2),…, t_in-C(k+N₂)]，℃；T_in-pre (k+1)为室内温度的预测序列，由式（1）计算而得，T_in-pre (k+1)= [t_in-pre(k+1), t_in-pre(k+2),…, t_in-pre(k+N₂)]，℃；σ₁、σ₂为权重参数；N₂为MPC控制时域。

1.3.2 改进型Adam算法

式（14）为仅与U^mpc(k)相关的二次函数，为求解该函数，本文提出一种改进Adam算法。其中Adam算法的更新求解过程如下^[33]：

${\theta }_{g}=\nabla L({U}_{g}^{mpc}(k))$

(15)

$\alpha _g^1 = {\beta _1}\alpha _{g - 1}^1 + (1 - {\beta _1}){\theta _g}$

(16)

$\alpha _g^2 = {\beta _2}\alpha _{g - 1}^2 + (1 - {\beta _2}){\theta _g}^2$

(17)

$\hat \alpha _g^1 = \alpha _g^1/(1 - {\beta _1}),\hat \alpha _g^2 = \alpha _g^2/(1 - {\beta _2})$

(18)

$U_{g + 1}^{mpc}(k) = U_g^{mpc}(k) - \eta \frac{{\hat \alpha _g^1}}{{\sqrt {\alpha _g^2} }}$

(19)

式中 $\nabla L$ (·)表示导数计算函数；g表示迭代次数；η表示学习率；θ表示导数，对应u^mpc(k),…,u^mpc(k+N₂-1)的偏导数为θ⁰,…, ${\theta ^{{N_2} - 1}}$ ；α¹、α²、 ${\hat \alpha ^1}$ 、 ${\hat \alpha ^2}$ 分别表示一阶动量、二阶动量以及经偏差纠正后的一阶动量、二阶动量；β₁、β₂为平滑参数，分别取值0.9、0.999。

AdaBelief算法是在Adam算法的基础上加入了置信度机制。该算法可以在函数优化过程中更精确的调整学习率，可用于处理复杂任务，其计算过程与Adam算法一致，仅对式（17）做出如下更改：

$\alpha _g^2 = {\beta _2}\alpha _{g - 1}^2 + (1 - {\beta _2}){({\theta _g} - \alpha _g^1)^2}$

(20)

Nesterov算法利用虚拟梯度机制对计算过程进行加速收敛，提高了计算速度，该算法更新过程如下：

${\theta }_{g}=\nabla L（{U}_{g}^{mpc}(k)-\eta {\beta }_{1}{\alpha }_{g-1}^{1}）$

(21)

$\alpha _g^1 = {\beta _1}\alpha _{g - 1}^1 + {\theta _g}$

(22)

$U_{g + 1}^{mpc}(k) = U_g^{mpc}(k) - \eta \alpha _g^1$

(23)

本文将AdaBelief算法的置信度机制式（20）与Nesterov算法的虚拟梯度机制式（21）引入到Adam中，形成改进Adam算法，计算过程如下：

${\theta }_{g}=\nabla L（{U}_{g}^{mpc}(k)-\eta {\beta }_{1}{\alpha }_{g-1}^{1}）$

(24)

$\alpha _g^1 = {\beta _1}\alpha _{g - 1}^1 + (1 - {\beta _1}){\theta _g}$

(25)

$\alpha _g^2 = {\beta _2}\alpha _{g - 1}^2 + (1 - {\beta _2}){({\theta _g} - \alpha _g^1)^2}$

(26)

$\hat \alpha _g^1 = \alpha _g^1/(1 - {\beta _1}),\hat \alpha _g^2 = \alpha _g^2/(1 - {\beta _2})$

(27)

$U_{g + 1}^{mpc}(k) = U_g^{mpc}(k) - \eta \frac{{\hat \alpha _g^1}}{{\sqrt {\alpha _g^2} }}$

(28)

1.3.3 算法适用性

在改进型Adam算法的计算过程中，需要求取目标函数的导数。目标函数为式（14），对U^mpc(k)求导如式（29）所示：

$\begin{split} \theta = \frac{{\partial j(k)}}{{\partial {U^{mpc}}(k)}} =\;& {\sigma _2}{U^{mpc}}(k) - {\sigma _1}{\left( {\frac{{\partial {T_{in - pre}}(k + 1)}}{{\partial {U^{mpc}}(k)}}} \right)^{\mathrm{T}}}\cdot\\ & ({T_{in - C}}(k + 1) - {T_{in - pre}}(k + 1)) \end{split}$

(29)

式中T为转置，可以发现，使用改进Adam算法的关键在于求解预测模型输出的导数 $\partial$ T_in-pre (k+1)/ $\partial$ U^mpc(k)。由于在GRU-Attention网络训练过程中激活函数sigmoid、tanh与softmax均是连续且可导， $\partial$ T_in-pre (k+1)/ $\partial$ U^mpc(k)的雅可比矩阵存在^[38]，即式（29）可解。对预测模型的求导过程过于复杂，因此在计算过程中采用中心差分方法近似求得导数，计算式为

$\theta = \frac{{j(U_g^{mpc}(k) + h) - j(U_g^{mpc}(k) - h)}}{{2h}}$

(30)

式中h表示一个小的步长。

使用改进型Adam算法进行优化求解步骤如下所示：

1）输入参考轨迹T_in-C，初始化计算参数如下：学习率η为0.05；控制时域N₂为5；步长h为0.05；改进Adam算法迭代次数g取值30；解U^mpc(k) =[u^mpc(k), u^mpc(k+1),…,u^mpc(k+4)]。

2）根据式（30）计算k时刻下的导数值θ，对应解[u^mpc(k), u^mpc(k+1),…,u^mpc(k+4)]的偏导数为θ⁰，θ¹，θ²，θ³，θ⁴。

3）判断θ⁰，…，θ⁴是否为0，是则执行第6）步，否则执行第4）步。

4）根据式（24）～（28）对U^mpc(k)进行更新。

5）计算目标函数值j(k)，并判断是否达到迭代次数，是则执行第6）步，否则执行第2）步。

6）输出最优控制序列，U^mpc(k)=[u^mpc(k), u^mpc(k+1),…,u^mpc(k+4)]。

1.4 试验材料与方法

试验在北京市某海鲜菇菌种植公司开展，通过传感器对室外温湿度、太阳辐射量、空调开启状态、室内温度、新风开启状态等状态参数进行监测。由式（14）可知，MPC在进行优化求解时需要考虑系统参数的未来状态，因此本文数据采用特征为太阳辐射量、室外温度、空调开启时长与室内温度。

试验日期为2022年5月11日—2022年9月11日。为便于展示，选择8月21日—8月25日间数据，空调开启时长以天（d）为单位，室内温度平均以小时（h）为单位。室外温度、太阳辐射、室内温度、空调开启时长如图2所示。

图 2 数据采集

Figure 2. Data collection

下载: 全尺寸图片幻灯片

本文以10 min作为一个控制周期，数据采集完成后，数据处理步骤如下：

1）为避免不同量纲对模型预测结果产生不利影响，需对所有采集数据进行Max-Min归一化处理。

2）将处理后的数据T_in、U、D，根据式（1）输入至GRU-Attention预测模型中，其中D包含室外温度与太阳辐射参数，根据文章1.2节所述训练基于物理约束的GRU-Attention模型，验证本文所用预测模型对菇房室内温度的预测效果。

3）根据1.3.3节所述，进行MPC的滚动优化环节，选择改进Adam算法，对目标函数进行求解计算，验证该算法性能。

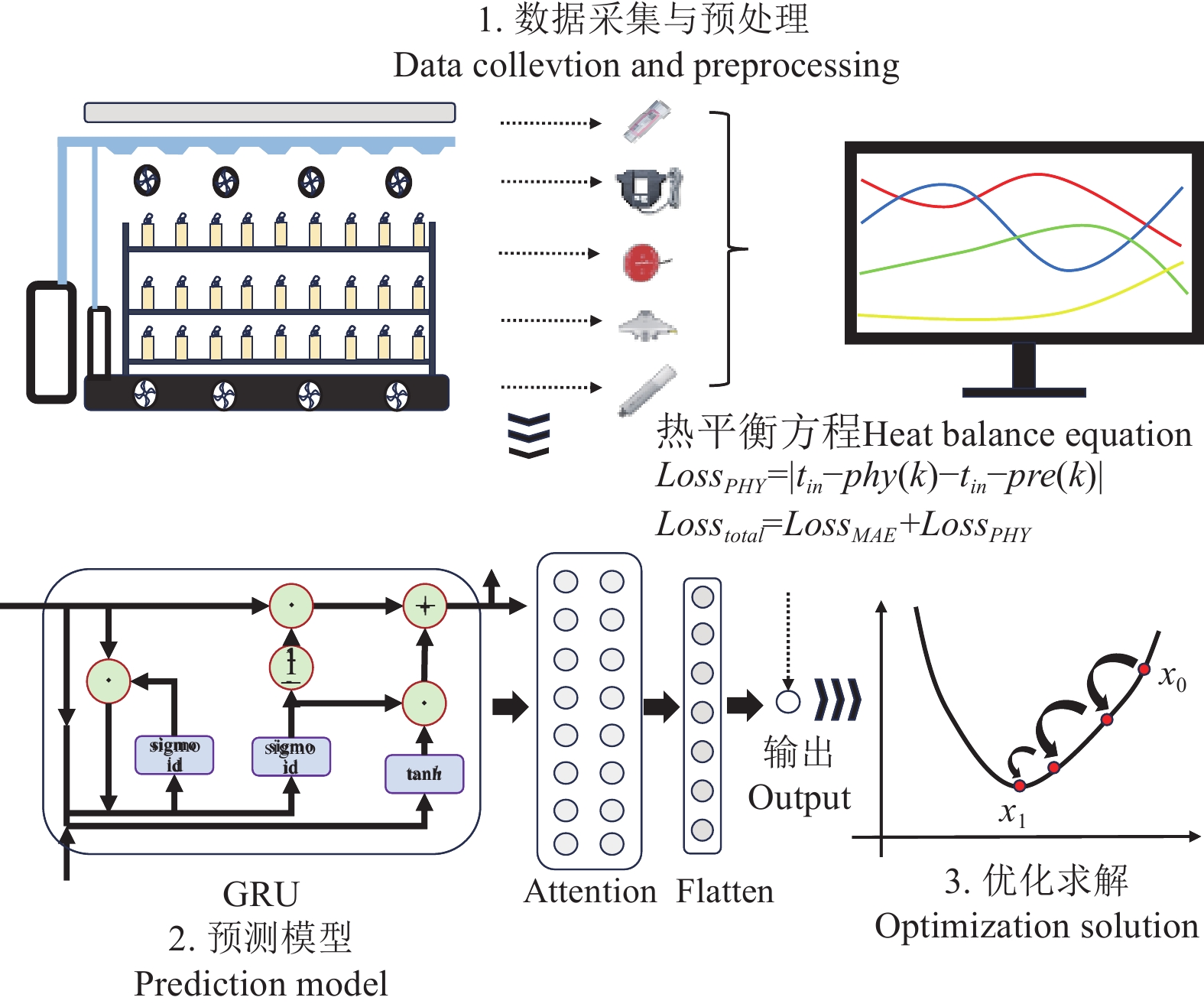
流程如图3所示。

图 3 节能控制方法流程

注：Flatten层将注意力（Attention）机制输出的多维数组转化为1维数组；x₀、x₁分别表示优化前、后的数值。

Figure 3. Process of energy-saving control methods

Note: The flatten layer converts the multi-dimensional array output by the attention mechanism into a 1-dimensional array, x₀ and x₁ represent the values before and after optimization respectively.

下载: 全尺寸图片幻灯片

2. 结果与分析

2.1 模型预测结果分析

GRU网络具有优秀的温度预测能力，在使用过程中通常与卷积神经网络（convolutional neural network, CNN）^[21]、注意力机制^[39]搭配使用，本文所提出预测模型为基于物理约束的GRU-Attention模型（简称PHY-GRU-A），可视为GRU网络的衍生结构，为验证其预测效果，与其它常用GRU网络的衍生结构进行对比分析。其中，通过优化算法对模型超参数进行寻优，各模型中，GRU层数均为1、神经元个数均为18；迭代次数为500代，优化器利用Adam，学习率取值为0.001；涉及CNN的网络中CNN层数均为1、卷积核个数均为15。训练集、验证集与测试集的数据分配比例均为6:2:2。对测试集的预测结果如表1所示。

表 1 不同模型的预测效果

Table 1. Prediction effect of different models

模型 Model	拟合优度 Goodness of fit R²	运算时长 Computation time/s
GRU	0.715	15
GRU-A	0.746	15
CNN-GRU	0.727	32
CNN-GRU-A	0.827	32
PHY-GRU-A	0.841	16
注：GRU-A为GRU网络与Attention机制组合而成，CNN-GRU为CNN与GRU与Attention机制组合而成，CNN-GRU-A为CNN、GRU与Attention机制组合而成，PHY-GRU-A为在GRU-A网络的基础上添加物理约束。
Note: Gru-A is A combination of GRU network and Attention mechanism, CNN-GRU is A combination of CNN and GRU and Attention mechanism, and CNN-GRU-A is a combination of CNN, GRU and Attention mechanism, PHY-GRU-A indicates that physical constraints are added to the GRU-A network.

下载: 导出CSV

| 显示表格

由表1可知，在GRU-A的基础上加入卷积神经网络或物理约束均可有效提高模型的预测性能。由于CNN中存在复杂的多重卷积运算，导致含CNN网络的模型运算时长大幅增加。而PHY-GRU-A仅在损失函数中增加菇房热平衡相关的数乘运算，因此运算时长相较于CNN-GRU-A降低了50%；在拟合优度方面，相较于传统GRU网络提升了18%。

为验证模型的泛化性能，在原始数据集中随机抽取4 d，利用PHY-GRU-A进行温度预测试验，验证PHY-GRU-A模型的预测效果（图4）。结果表明：随机抽取的4 d预测精度的拟合优度（R²）均在0.8以上，均方根误差RMSE控制在0.10 ℃以内，预测效果良好。

图 4 模型预测效果

注：RMSE为均方根误差。

Figure 4. Model prediction effect

Note: RMSE is root mean square error.

下载: 全尺寸图片幻灯片

2.2 算法优化效果分析

运算时长与求解精度是滚动优化步骤中最重要的两个参数，运算时长影响着控制策略对被控对象的反应速度，而求解精度则会影响被控对象的下一控制周期的初始状态。因此，为验证改进型Adam的计算性能，本节通过运算时长与求解精度对其进行评估。参与到评估中的还有带精英策略的快速非支配排序遗传算法（non-dominated sorting genetic algorithm Ⅱ, NSGA-Ⅱ）、模型预测路径积分算法（model predictive path integral, MPPI）、GD^[31]、Adam，其中：

MPPI作为模型预测控制的一种变体，将路径积分的概念与模型预测控制结合，其考虑每个时间步长上的所有轨迹，并以加权平均的方法计算最优控制序列^[40-41]。

NSGA-Ⅱ在传统遗传算法的基础上加入了精英策略与非支配排序算法，显著降低了算法的运算时长^[42]。由于其出色的性能，ASCIONE等^[43]将其应用在MPC控制中。

在试验时，预测模型均采用PHY-GRU-A，单个周期对比结果如表2。

表 2 不同算法优化性能分析

Table 2. Optimization performance analysis of different algorithms

算法类别 Class of algorithm	适应度值 Fitness value j(k)	运算时长 Computation time/s
MPPI	0.915	72
NSGA-Ⅱ	0.757	250
GD	0.919	45
Adam	0.801	47
改进Adam	0.751	47
注：MPPI为模型预测路径积分算法，NSGA-Ⅱ为带精英策略的快速非支配排序遗传算法，GD为梯度下降算法，Adam为自适应矩估计算法。
Note: MPPI is a model prediction path integral algorithm, NSGA-Ⅱ is a fast non-dominated sorting genetic algorithm with elite strategy, GD is gradient descent algorithm, Adam is an adaptive moment estimation algorithm.

下载: 导出CSV

| 显示表格

随后，以7月17日气象参数条件为支撑进行仿真，控制效果如图5a所示。

图 5 不同算法的仿真性能对比

注：图示结果为将上述5种算法应用于MPC求解。其中改进Adam-MPC为将改进Adam算法应用于MPC求解；Adam-MPC为将Adam 算法应用于MPC求解；GD-MPC为将GD算法应用于MPC求解；NSGA-II-MPC为将NSGA-II算法应用于MPC求解；MPPI-MPC为将MPPI算法应用于MPC求解。

Figure 5. Comparison of simulation performance of different algorithms

Note: The results show that the above 5 algorithms are applied to MPC solution. The improved Adam-MPC is the application of the improved Adam algorithm to MPC solution; Adam-MPC is the application of Adam algorithm to MPC solution GD-MPC is the application of GD algorithm to MPC solution; NSGA-II-MPC is the application of NSGA-II algorithm to MPC solution; MPPI-MPC is the application of MPPI algorithm to MPC solution.

下载: 全尺寸图片幻灯片

从箱线图分布情况可以看出，利用NSGA-Ⅱ、Adam、改进Adam算法进行求解的MPC方法控制效果相似且要优于MPPI与GD算法。其中，NSGA-Ⅱ-MPC方法的室内温度在14.42～14.59 ℃之间，25%～75%在14.49～14.54 ℃之间，平均温度为14.50 ℃；Adam-MPC方法的室内温度在14.42～14.61 ℃之间，25%～75%在14.49～14.54 ℃之间，平均温度为14.51 ℃；改进Adam-MPC方法的室内温度在14.42～14.58 ℃之间，25%～75%在14.48～14.52 ℃之间，平均温度为14.50 ℃；如图5b所示，利用改进Adam～MPPI算法的空调开启时长依次为627、637、621、619、621 min。

整体上5种算法下的MPC控制效果相近，结合表2中适应度值计算情况与算法运算时长，改进Adam算法下的MPC控制效果要略优于Adam，适应度值降低了6%，并且运算时长相较于NSGA-Ⅱ，减少了81%。因此改进Adam算法更适用本文的短周期寻优控制。

2.3 MPC模型跟踪性能评估

为评价本文MPC模型对参考轨迹的跟踪性能，预设参考轨迹，具体分别在第6、12、18 h对设定温度进行更改。阈值控制方法下，温度上下限为参考轨迹±0.50 ℃。温度控制效果如图6所示，统计后得出，阈值控制方法与参考轨迹的RMSE为0.30 ℃，且有50 min的平均温度超过设定范围，而本方法与参考轨迹的RMSE为0.11 ℃，由此可见经MPC计算后的室内温度对参考轨迹具有良好的跟踪效果。

图 6 控制效果

Figure 6. Control effect

下载: 全尺寸图片幻灯片

本文控制时域N₂为5，由式（14）可知，MPC方法会考虑未来5个控制周期内的参考轨迹变化。如图7中，空调开启时长总会在参考轨迹变化的前1 h发生变化，以第6 h升温为例，第5 h内提前大幅缩短控制时长。因此，本文提出的MPC模型具有良好地全局控制效果。

图 7 MPC空调开启时长

Figure 7. MPC air conditioner opening time

下载: 全尺寸图片幻灯片

综上所述，本文所提出的MPC模型与文献[44]研究一致，可以在控制时域内根据参考轨迹的变化提前调整控制量，确保室内温度实时跟踪参考轨迹，相较于阈值控制方法，跟踪精度提高63%。

2.4 MPC模型节能效果分析

为验证本文MPC模型的节能效果，选取8月20日—8月25日连续5 d进行仿真试验，从控制精度与能耗两方面与采用阈值控制方法进行对比分析。在8月21日—8月23日之间菇房室内温度设定阈值范围为14.20～15.20 ℃，在8月24日根据海鲜菇生长特性，更改参考阈值范围为14.00～15.00 ℃。取其设定范围中值作为参考轨迹。控制效果如图8所示。

图 8 MPC模型5 d的仿真结果

Figure 8. 5 days simulation results of MPC model

下载: 全尺寸图片幻灯片

图8a反映了MPC方法与阈值控制方法下的室内温度分布情况：

1）8月21日—8月23日，阈值控制方法下的室内平均温度分别为14.72、14.71、14.78 ℃，相较于设定中值的RMSE为0.27、0.16、0.17 ℃；MPC方法下的平均温度分别为14.71、14.71、14.72 ℃，相较于设定中值的RMSE为0.06、0.06、0.05 ℃。

2）8月24日—8月25日，阈值控制方法下的室内平均温度分别为14.54、14.44 ℃，相较于设定中值的RMSE为0.14、0.24 ℃；MPC方法的平均温度均为14.53 ℃，相较于中值的RMSE均为0.04 ℃。

因此，在菇房温度的控制精度方面，与阈值控制法相比，MPC方法的RMSE分别降低了78%、63%、71%、71%、83%，平均降低了73%，且无超出温度设置范围的情况。

图8b为两种控制方法的空调开启时长对比情况，相较于阈值控制法，MPC方法的空调开启时长分别降低了19%、11%、12%、5%、11%，平均节能率达12%。本文提出的MPC方法在节能效果上优于文献[45]中9%的节能率，并且在计算速度和实时控制效果方面，更能满足工厂化食用菌环境控制的需求。

由此可见，本文所构建的MPC方法对设定温度的跟踪能力强，同时相较于阈值开关法MPC法表现出了明显的节能效果。

3. 结　论

1）提出了基于物理约束的GRU-Attention预测模型PHY-GRU-A，将菇房室内热平衡纳入损失函数中，提高了预测精度。在4 d的温度预测上，其拟合优度（R²）均在0.8以上，均方根误差RMSE在0.10 ℃以内，运算时长仅为16 s。

2）本文基于自适应矩估计算法Adam，引入置信度计算机制与虚拟梯度机制，提出了改进型Adam。在模型预测控制的滚动优化过程中，改进型Adam算法适应度值为0.751，单个控制周期内其运算时长仅需47 s。

3）所构建的模型预测控制方法对参考轨迹具有良好的跟踪效果，其通过在控制时域内的全局控制对参考轨迹进行实时跟踪，跟踪精度可提高63%。与当前食用菌工厂普遍使用的阈值控制法相比，在控制精度方面均方根误差RMSE平均降低了73%，在空调能耗方面平均节省了12%。

图 1 GRU神经元结构

注：x_k为输入；h_k-1为k-1周期的隐藏状态；y_k为输出；h_k为隐藏状态； r_k为重置门；z_k为更新门； ${\tilde h_k}$ 为候选隐藏状态；Sigmoid、tanh为激活函数，下同。

Figure 1. Gated recurrent unit（GRU）neuron structure

Note: x_k is the input; h_k-1 is the hidden state of the k-1 period; y_k is the output; h_k is the hidden state; r_k is the reset gate; z_k is the update gate; ${\tilde h_k}$ is the candidate hidden state; Sigmoid and tanh are activation functions, the same below.

下载: 全尺寸图片幻灯片

图 2 数据采集

Figure 2. Data collection

下载: 全尺寸图片幻灯片

图 3 节能控制方法流程

注：Flatten层将注意力（Attention）机制输出的多维数组转化为1维数组；x₀、x₁分别表示优化前、后的数值。

Figure 3. Process of energy-saving control methods

下载: 全尺寸图片幻灯片

图 4 模型预测效果

注：RMSE为均方根误差。

Figure 4. Model prediction effect

Note: RMSE is root mean square error.

下载: 全尺寸图片幻灯片

图 5 不同算法的仿真性能对比

Figure 5. Comparison of simulation performance of different algorithms

下载: 全尺寸图片幻灯片

图 6 控制效果

Figure 6. Control effect

下载: 全尺寸图片幻灯片

图 7 MPC空调开启时长

Figure 7. MPC air conditioner opening time

下载: 全尺寸图片幻灯片

图 8 MPC模型5 d的仿真结果

Figure 8. 5 days simulation results of MPC model

下载: 全尺寸图片幻灯片

表 1 不同模型的预测效果

Table 1 Prediction effect of different models

模型 Model	拟合优度 Goodness of fit R²	运算时长 Computation time/s
GRU	0.715	15
GRU-A	0.746	15
CNN-GRU	0.727	32
CNN-GRU-A	0.827	32
PHY-GRU-A	0.841	16
注：GRU-A为GRU网络与Attention机制组合而成，CNN-GRU为CNN与GRU与Attention机制组合而成，CNN-GRU-A为CNN、GRU与Attention机制组合而成，PHY-GRU-A为在GRU-A网络的基础上添加物理约束。
Note: Gru-A is A combination of GRU network and Attention mechanism, CNN-GRU is A combination of CNN and GRU and Attention mechanism, and CNN-GRU-A is a combination of CNN, GRU and Attention mechanism, PHY-GRU-A indicates that physical constraints are added to the GRU-A network.

下载: 导出CSV

表 2 不同算法优化性能分析

Table 2 Optimization performance analysis of different algorithms

算法类别 Class of algorithm	适应度值 Fitness value j(k)	运算时长 Computation time/s
MPPI	0.915	72
NSGA-Ⅱ	0.757	250
GD	0.919	45
Adam	0.801	47
改进Adam	0.751	47
注：MPPI为模型预测路径积分算法，NSGA-Ⅱ为带精英策略的快速非支配排序遗传算法，GD为梯度下降算法，Adam为自适应矩估计算法。
Note: MPPI is a model prediction path integral algorithm, NSGA-Ⅱ is a fast non-dominated sorting genetic algorithm with elite strategy, GD is gradient descent algorithm, Adam is an adaptive moment estimation algorithm.

下载: 导出CSV

参考文献(45)

[1]	董浩然,于海龙,姜宁,等. 中国食用菌工厂化生产发展现状及趋势[J]. 食药用菌,2024,32(1):1-9. DONG Haoran, YU Hailong, JIANG Ning, et al. The current status and trends of the development of industrialized production of edible mushrooms in China[J]. Edible and Medicinal Mushrooms, 2024, 32(1): 1-9. (in Chinese with English abstract)
[2]	AWTONIUK M, DANIUM M, KOMARCHUK D, et al. Predictive modelling for air temperature and humidity in a mushroom production process[J]. IOP Conference Series: Materials Science and Engineering, 2019, 710(1): 012011. doi: 10.1088/1757-899X/710/1/012011
[3]	SHI H S, CHEN Q. Building energy management decision-making in the real world: A comparative study of HVAC cooling strategies[J]. Journal of Building Engineering, 2021, 33: 101869. doi: 10.1016/j.jobe.2020.101869
[4]	SETIAWAIT D A, UTOMO S G, PUTRA G M D, et al. Design of temperature and humidity control system on oyster mushroom plant house based on Internet of Things (IoT)[J]. IOP Conference Series: Earth and Environmental Science, 2021, 712(1): 012002. doi: 10.1088/1755-1315/712/1/012002
[5]	高立婷,戴思慧,徐新明,等. 温室温湿度耦合控制方法研究[J]. 农机化研究,2021,43(12):24-30. doi: 10.3969/j.issn.1003-188X.2021.12.005 GAO Liting, DAI Sihui, XU Xinming, et al. Research on temperature and humidity coupling control method of greenhouse[J]. Journal of Agricultural Mechanization Research, 2021, 43(12): 24-30. (in Chinese with English abstract) doi: 10.3969/j.issn.1003-188X.2021.12.005
[6]	FU Q M, HAN Z C, CHEN J P, et al. Applications of reinforcement learning for building energy efficiency control: A review[J]. Journal of Building Engineering, 2022, 50: 104165. doi: 10.1016/j.jobe.2022.104165
[7]	魏东,韩少然,冉义兵,等. 数据中心制冷系统非线性模型预测控制[J]. 控制与决策,2024,39(4):1240-1250. WEI Dong, HAN Shaoran, RAN Yibing, et al. Nonlinear model predictive control for data center cooling systems[J]. Control and Decision, 2024, 39(4): 1240-1250. (in Chinese with English abstract)
[8]	SHA L, JIANG Z W, SUN H J. A control strategy of heating system based on adaptive model predictive control[J]. Energy, 2023, 273: 127192. doi: 10.1016/j.energy.2023.127192
[9]	张宇,李书琴. 低资源场景下苹果种植领域实体关系联合抽取模型[J]. 农业工程学报,2024,40(16):188-195. doi: 10.11975/j.issn.1002-6819.202403214 ZHANG Yu, LI Shuqin. Joint extraction model for entity relationships using reinforcement learning in low resource scenarios[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2024, 40(16): 188-195. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.202403214
[10]	DARBY M L, HARMSE M, NIKOLAOU M. MPC: Current practice and challenges[J]. Control Engineering Practice, 2012, 20(4): 328-42. doi: 10.1016/j.conengprac.2011.12.004
[11]	杜太行,刘德,孙曙光,等. 基于模型预测的日光温室温度优化控制[J]. 中国测试,2022,48(1):85-91,167. DU Taihang, LIU De, SUN Shuguang, et al. Optimal temperature control of solar greenhouse based on MPC method[J]. China Measurement & Test, 2022, 48(1): 85-91,167. (in Chinese with English abstract)
[12]	GONG L Y, YU M, KOLLIAS S. Optimizing crop yield and reducing energy consumption in greenhouse control using PSO-MPC algorithm[J]. Algorithms, 2023, 16(5): 243. doi: 10.3390/a16050243
[13]	DU Y H, ZHOU Z H, ZHAO J. Multi-regional building energy efficiency intelligent regulation strategy based on multi-objective optimization and model predictive control[J]. Journal of Cleaner Production, 2022, 349: 131264. doi: 10.1016/j.jclepro.2022.131264
[14]	侯峰,芦岩,何汀,等. 太阳能多热源热泵干燥系统多目标优化[J]. 农业工程学报,2024,40(19):281-291. doi: 10.11975/j.issn.1002-6819.202404021 HOU Feng, LU Yan, HE Ting, et al. Multi-objective optimization of a solar assisted multi-heat source heat pump drying system[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2024, 40(19): 281-291. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.202404021
[15]	DRGONA J, PICARD D, HELSEN L. Cloud-based implementation of white-box model predictive control for a GEOTABS office building: A field test demonstration[J]. Journal of Process Control, 2020, 88: 63-77. doi: 10.1016/j.jprocont.2020.02.007
[16]	KNUDSEN M D, PETERSEN S. Economic model predictive control of space heating and dynamic solar shading[J]. Energy and Buildings, 2020, 209: 109661. doi: 10.1016/j.enbuild.2019.109661
[17]	JEON B K, KIM E J. White-model predictive control for balancing energy savings and thermal comfort[J]. Energies, 2022, 15(7): 2345. doi: 10.3390/en15072345
[18]	JUNG D H, KIM H J, KIM J Y, et al. Model predictive control via output feedback neural network for improved multi-window greenhouse ventilation control[J]. Sensors, 2020, 20(6): 1756. doi: 10.3390/s20061756
[19]	CHEN Y B, GAO J X, YANG J Z, et al. An hour-ahead predictive control strategy for maximizing natural ventilation in passive buildings based on weather forecasting[J]. Applied Energy, 2023, 333: 120613. doi: 10.1016/j.apenergy.2022.120613
[20]	张观山,丁小明,何芬,等. 基于LSTM-AT的温室空气温度预测模型构建[J]. 农业工程学报,2024,40(18):194-201. doi: 10.11975/j.issn.1002-6819.202404199 ZHANG Guanshan, DING Xiaoming, HE Fen, et al. Predicting greenhouse air temperature using LSTM-AT[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2024, 40(18): 194-201. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.202404199
[21]	赵全明,宋子涛,李奇峰,等. 基于CNN-GRU的菇房多点温湿度预测方法研究[J]. 农业机械学报,2020,51(9):294-303. ZHAO Quanming, SONG Zitao, LI Qifeng, et al. Research on multi-point Temperature and humidity prediction method of mushroom house based on CNN-GRU[J]. Transactions of the Chinese Society for Agricultural Machinery, 2019, 51(9): 294-303. (in Chinese with English abstract)
[22]	CHEN X Z, HAN X, MALKAWI A, et al. Adaptive model predictive control with ensembled multi-time scale deep-learning models for smart control of natural ventilation[J]. Building and Environment, 2023, 242: 110519. doi: 10.1016/j.buildenv.2023.110519
[23]	GUIDOTTI R, MONREALE A, RUGGIERI S, et al. A survey of methods for explaining black box models[J]. ACM Computing Surveys (CSUR), 2018, 51(5): 1-24.
[24]	WANG H C, BO S, ZHU C Z, et al. A zoned group control of indoor temperature based on MPC for a space heating building[J]. Energy Conversion and Management, 2023, 290: 117196. doi: 10.1016/j.enconman.2023.117196
[25]	YAO Y, SHEKHAR D K. State of the art review on model predictive control (MPC) in heating ventilation and air-conditioning (HVAC) field[J]. Building and Environment, 2021, 200: 107952. doi: 10.1016/j.buildenv.2021.107952
[26]	DRGONA J, TUOR A R, CHANDAN V, et al. Physics-constrained deep learning of multi-zone building thermal dynamics[J]. Energy and Buildings, 2021, 243: 110992. doi: 10.1016/j.enbuild.2021.110992
[27]	HAMP Q, LEVIHN F. Model predictive control for dynamic indoor conditioning in practice[J]. Energy and Buildings, 2022, 277: 112548. doi: 10.1016/j.enbuild.2022.112548
[28]	刘文龙,郭锐,赵静一. 基于预瞄模型的农机路径跟踪预测控制方法[J]. 农业工程学报,2023,39(17):39-50. doi: 10.11975/j.issn.1002-6819.202303109 LIU Wenlong, GUO Rui, ZHAO Jingyi. Predictive control method for the path tracking of agricultural machinery based on preview model[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(17): 39-50. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.202303109
[29]	TAMASHIRO K, OMINE E, KRISHNAN N, et al. Optimal components capacity based multi-objective optimization and optimal scheduling based MPC-optimization algorithm in smart apartment buildings[J]. Energy and Buildings, 2023, 278: 112616. doi: 10.1016/j.enbuild.2022.112616
[30]	ARUTA G, ASCIONE F, BIANCO N, et al. Optimizing heating operation via GA- and ANN-based model predictive control: Concept for a real nearly-zero energy building[J]. Energy and Buildings, 2023, 292: 113139. doi: 10.1016/j.enbuild.2023.113139
[31]	YOO H J, NGUYEN T T, KIM H M. MPC with constant switching frequency for inverter-based distributed generations in microgrid using gradient descent[J]. Energies, 2019, 12(6): 1156. doi: 10.3390/en12061156
[32]	汪小旵,吴忠贤,孙晔,等. 基于叶绿素荧光成像技术的番茄苗热害胁迫智能识别方法[J]. 农业工程学报,2022,38(7):171-179. doi: 10.11975/j.issn.1002-6819.2022.07.019 WANG Xiaochan, WU Zhongxian, SUN Ye, et al. Intelligent identification of heat stress in tomato seedlings based on chlorophyll fluorescence imaging technology[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2022, 38(7): 171-179. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.2022.07.019
[33]	ZHUANG J T, TANG T, DING Y F, et al. AdaBelief optimizer: Adapting stepsizes by the belief in observed gradients[EB/OL]. [2024-10-05]. https//doi.org/10.48550/arXiv.2010.07458.
[34]	张铮,贾香港,张泽扬,等. 融合IDA-GRU和IIDW的水产养殖溶解氧时空预测模型[J]. 农业工程学报,2023,39(21):161-171. doi: 10.11975/j.issn.1002-6819.202307067 ZHANG Zheng, JIA Xianggang, ZHANG Zeyang, et al. Spatiotemporal prediction model of dissolved oxygen in aquaculture intergrating IDA-GRU and IIDW[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2023, 39(21): 161-171. (in Chinese with English abstract) doi: 10.11975/j.issn.1002-6819.202307067
[35]	PAN M Y, ZHOU H N, CAO J Y, et al. Water level prediction model based on GRU and CNN[J]. IEEE Access, 2020, 8: 60090-60100. doi: 10.1109/ACCESS.2020.2982433
[36]	刘国海,孙文卿,吴振飞,等. 基于Attention-GRU的短期光伏发电功率预测[J]. 太阳能学报,2022,43(2):226-232. LIU Guohai, SUN Wenqing, WU Zhenfei, et al. Short-term photovoltaic power forecasting based on attention-GRU model[J]. Acta Energiae Solaris Sinica, 2022, 43(2): 226-232. (in Chinese with English abstract)
[37]	承银辉. 食用菌菇房环境CFD分析及通风结构优化研究[D]. 镇江:江苏大学,2020. CHENG Yinhui. CFD Analysis of Environment of Edible Mushroom House and Optimization of Ventilation Structure[D]. Zhenjiang: Jiangsu University, 2020. (in Chinese with English abstract)
[38]	HUANG K K, WEI K, LI F B, et al. LSTM-MPC: A deep learning based predictive control method for multimode process control[J]. IEEE Transactions on Industrial Electronics, 2023, 70(11): 11544. doi: 10.1109/TIE.2022.3229323
[39]	SONG J C, XUE G X, MA Y P, et al. An indoor temperature prediction framework based on hierarchical attention gated recurrent unit model for energy efficient buildings[J]. IEEE Access, 2019, 7: 157268-157283. doi: 10.1109/ACCESS.2019.2950341
[40]	QU Y, CHU H Q, GAO S H, et al. RL-Driven MPPI: Accelerating online control laws calculation with offline policy[J]. IEEE Transactions on Intelligent Vehicles, 2024, 9(2): 3605-3616. doi: 10.1109/TIV.2023.3348134
[41]	HOMBURGER H, WIRTENSOHN S, DIEHL M, et al. Feature-based MPPI control with applications to maritime systems[J]. Machines, 2022, 10(10): 900. doi: 10.3390/machines10100900
[42]	VERMA S, PANT M, SNASEL V. A comprehensive review on NSGA-II for multi-objective combinatorial optimization problems[J]. IEEE Access, 2021, 9: 57757-57791. doi: 10.1109/ACCESS.2021.3070634
[43]	ASCIONE F, MASI R F D, FESTA V, et al. Optimizing space cooling of a nearly zero energy building via model predictive control: Energy cost vs comfort[J]. Energy and Buildings, 2023, 278: 112664. doi: 10.1016/j.enbuild.2022.112664
[44]	BAHRAMNIA P, ROSTAMI S M H, WANG J, et al. Modeling and controlling of temperature and humidity in building heating, ventilating, and air conditioning system using model predictive control[J]. Energies, 2019, 12(24): 4085.
[45]	邹宇航,王明飞,张馨,等. 基于模型预测控制的工厂化菇房空调调控方法[J]. 中国农机化学报,2024,45(6):98-105. ZOU Yuhang, WANG Mingfei, ZHANG Xin, et al. Control method of factory mushroom room air conditioning based on model predictive control[J]. Journal of Chinese Agricultural Mechanization, 2024, 45(6): 98-105. (in Chinese with English abstract)